Тема 6. Статистическое изучение связей и зависимостей
Все явления общественной жизни существуют не изолировано, а в неразрывной связи, т.е. зависят одно от другого. При этом выделяются факторные (х) и результативные (у) признаки.
Для количественных признаков зависимость между отдельными явлениями могут быть:
- функциональными, когда определенному значению одной переменной, фактору (х) отвечает четко определенное значение результативного признака (у);
- корреляционными (статистическими), когда с изменением факторного признака (х) изменяются групповые средние результативного признака (у).
Основным моментом в изучении связей между явлениями есть установление их сути на основе познания качественных характеристик явлений, их связей.
Наличие или отсутствие связей возможно выявить используя:
- метод аналитических группировок;
- графический метод;
- построение и анализ корреляционных таблиц;
- корреляционный анализ.
В корреляционно-регрессионном анализе линии регрессии имеются не в отдельных точках, как в аналитических группировках, а в каждой точке интервала изменения факторного значения (х). Линия регрессии изображается в виде определенной функции: у = f (x), которая называется уравнением регрессии, где у – теоретическое значение результативного признака.
Среди множества функций, наиболее распространенной в статистическом анализе является линейная 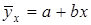 , что объясняется простотой и содержательностью.
, что объясняется простотой и содержательностью.
Для определения по данным парной корреляции параметров линейной регрессии надо решить систему нормальных уравнений для нахождения параметров а и b:
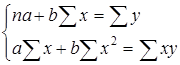
Иногда для нахождения параметров а и b используют способ определителей:
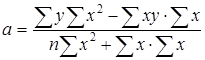 ;
; 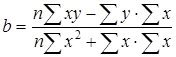
После нахождения параметров (а и b) уравнения это уже не уравнение регрессии, а корреляционное уравнение, которое возможно использовать в прогнозировании результативного признака (у) при определенном значении фактора (х): 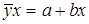
Методика расчетов изложена в таблице.
Таблица 3
| № п/п | Товарооборот, тыс. грн., х | Издержки обращения, тыс. грн., у | х2 | ху | у2 | Выравненное
значение
издержек
обращения,
тыс. грн.,
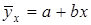
|
| ... | ||||||
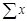
| 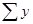
| 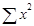
| 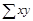
| 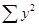
| 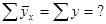
|
 2014-01-25
2014-01-25 760
760








