Способы нахождения обратной матрицы

1. С помощью определения. Этот способ будет изучен на практических занятиях.

2. С помощью алгебраических дополнений. Мы ограничимся квадратными матрицами порядка 3.

Обозначим A ⁱ_j – матрица, которая получается из матрицы A в результате вычёркивания i -ой строки и j -го столбца. Тогда её определитель называется минором, дополнительным к элементу: Mⁱ_j = det A ⁱ_j. Добавим теперь к этому минору знак «-», если сумма нечётна:

= (-1) ^{i + j} Mⁱ_j = (-1) ^{i + j} det A ⁱ_j.

Получившаяся величина называется алгебраическим дополнением элемента aⁱ_j. Тогда

A ^-1=.

Таким образом, для того, чтобы получить обратную матрицу, мы в матрице A на место каждого элемента ставим его алгебраическое дополнение, получившуюся матрицу транспонируем и умножаем на (det A)^-1.

Пример. A =.

Составляем и вычисляем алгебраические дополнения; при этом размещаем их на бумаге в виде матрицы, так чтобы каждое алгебраическое дополнение оказалось на месте соответствующего ему элемента:

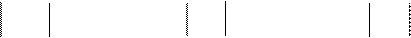= = -2, = - = -2, = = 8,

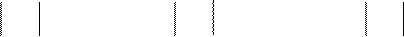= - = -2, = = -1, = - = 7

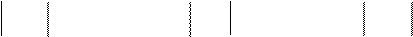= = 4, = - = 4, = = -18.

Например, при составлении мы вычёркивали вторую строку и первый столбец; затем мы приписали знак «-», потому, что 2+1 нечётно. Теперь найдём определитель det A. Он равен сумме произведений элементов любой строки (столбца) матрицы на их алгебраические дополнения. Возьмём вторую строку, т.к. в ней есть ноль:

det A = a ²₁ + a ²₂ + a ²₃ = 2·(-2) + (-2)·(-1) + 0·(-7) = -2.

При составлении A ^-1не забываем, что алгебраические дополнения выписываются по принципу «строчка – в столбец»:

A ^-1= - =.

Обязательно следует сделать проверку AA ^-1= E:

= =.

2. С помощью элементарных преобразований строк матрицы.

Этот способ является более эффективным, чем предыдущий, только если числа в матрице являются достаточно небольшими по модулю. Мы выписываем рядом с матрицей A единичную матрицу:

.

Затем мы совершаем элементарные преобразования строк этой матрицы, с целью привести её левую часть к виду единичной матрицы. Тогда на месте правой части получится матрица A ^-1.

Пример. A =.

Сначала мы пытаемся занулить все элементы в левой части, стоящие ниже диагонали. Затем зануляем элементы стоящие выше диагонали. Предполагается, что читатели уже знакомы с подобными действиями и использовали эти действия при решении систем линейных уравнений или при вычислении определителей. В отличие от последнего случая, мы можем ещё умножать строку на любое число, не равное нулю.

~ ~

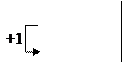
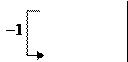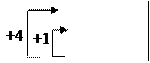
~ ´(-1) ~

´1/2~.

Итак, мы получили, что

A ^-1=.

Проверка:

= =.