Свойства умножения матриц

ПРИЛОЖЕНИЕ Умножение матриц. Обратная матрица.

Пусть A – строка, а B – столбец, состоящие из одинакового количества элементов:

A = (a ₁, a ₂,…, a_n) B =.

Тогда их произведением называется число

A · B = a ₁ b ¹ + a ₂ b ² +…+ a_nbⁿ.

Пусть A и B – две матрицы, причём длина строк матрицы A равна высоте столбцов матрицы B; другими словами, количество столбцов в A совпадает с количеством строк в B:

A =, B =.

Таким образом, размер матриц равен соответственно m ´ n и n ´ k. Обозначим

c_jⁱ = AⁱB_j = (aⁱ ₁, aⁱ ₂,…, aⁱ_n) = aⁱ ₁ b ¹ _j + aⁱ ₂ b ² _j +… + aⁱ_nbⁿ_j –

произведение i -ой строки матрицы A и j -го столбца матрицы B, i =1,…, m, j =1,…, k. Тогда элементы c_jⁱ образуют матрицу C размера m ´ k, которая называется произведением матриц A и B. Например, произведением матриц A и B размера 2´3 и 3´5 соответственно будет матрица C размера 2´5 и в ней элемент с ¹₃ получается в результате произведения первой строки матрицы A и третьего столбца матрицы B.

Пример 1. В результате произведения матрицы A размера 3´3 и столбца X высоты 3 (т.е. матрицы размера 3´1) получается матрица размера 3´1, т.е. столбец

=.

Если B =, то запись AX = B означает

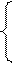
т.е. матричное равенство AX = B в развёрнутом виде представляет собой систему линейных уравнений.

Пример 2. = =.

Мы видим, что в результате произведения двух ненулевых матриц может получиться нулевая матрица.

1. Если определено AB, то произведение BA может быть вообще не определено. Даже если определены оба произведения AB и BA, то они могут иметь разный размер и их нельзя приравнивать. Если AB и BA имеют одинаковый размер, то может быть, что AB ¹ BA. Для матриц из примера 1 имеем

=.

Если AB = BA, то говорят, что матрицы A и B коммутируют.

2. A (B + С) = AB + AС,(A + B) С = AС + BС.

3. (l A) B = l(AB).

4. (AB) С = (BС).

Этот список свойств не является полным. Мы отметили лишь часть свойств.

Определение. Матрица X называется обратной к матрице A, если

AX = XA = E. (14)

Тогда пишем, что X = A ^-1. Матрица A называется обратимой, если существует обратная к ней матрица A ^-1.

Из определения сразу же следует, что A и X – квадратные матрицы одинакового размера и det A ·det X = det E = 1. Поэтому необходимым условием существования обратной к матрице A является det A ¹0. Примем без доказательства, что это условие является также и достаточным.