Основные показатели деятельности предприятий. Метод сопоставления параллельных данных

Пример 9.1

Метод сопоставления параллельных данных

Парная корреляция

Корреляционный анализ количественных признаков

Интерпретация результатов.

Теория корреляции начала разрабатываться во второй половине XIX в. Основоположниками теории корреляции являются английские ученые Френсис Гальтон и Карл Пирсон. В России их идеи получили развитие в трудах Александра Александровича Чупрова.

Корреляционный анализ позволяет решать следующие основные задачи:

1) выбор (с учетом специфики и природы анализируемых признаков) подходящего измерителя статистической связи;

2) оценка (с помощью точечной и интервальной оценок) его числового значения по имеющимся выборочным данным;

3) проверка гипотезы о том, что полученное числовое значение анализируемого измерителя связи действительно свидетельствует о наличии статистической связи;

4) определение структуры связей между компонентами исследуемого многомерного признака, сопоставляя каждой паре компонент двоичный ответ («связь есть» или «связи нет»).

Рассмотрим парную корреляцию.

Корреляционная связь между двумя признаками как частный случай стохастической связи выражается в вариации результативного признака Y, вызванной изменением определенного факторного признака X в условиях взаимодействия его с множеством других факторов, не учитываемых при исследовании, но имеющихся в реальности.

Простейшими методами обнаружения связи между двумя признаками являются метод сопоставления параллельных рядов, метод группировок и др.

При небольшом числе наблюдений наличие корреляционной связи между двумя признаками Х и Y часто можно выявить визуально, путем простого параллельного сопоставления их значений у отдельных единиц.

Для этого единицы наблюдения располагают по возрастанию значений факторного признака X и затем сравнивают с ним поведение значений результативного признака Y.

Таблица 9.1

(данные условные)

№ предприятия	Основные производственные фонды, млн. руб. xi	Валовой выпуск продукции, млн. руб. yi	Знаки отклонений от средней величины
			–	–
			–	–
			–	–
			–	–
			–	–
			+	+
			+	–
			+	+
			+	+
			+	+
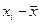
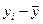
Итого

По данной таблице в целом можно сделать вывод, что чем больше стоимость основных фондов, тем больше валовой выпуск продукции, т.е. связь между рассматриваемыми факторным и результативным признаками прямая.

Такое «субъективное» суждение о наличии корреляционной связи обычно сопровождается расчетом того или иного показателя, используемого для измерения тесноты связи: коэффициента Фехнера, ранговых коэффициентов корреляции, линейного коэффициента корреляции и др.

Коэффициент Фехнера (коэффициент корреляции знаков) – простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений факторного и результативного признаков от своей средней величины. При этом во внимание принимаются не величины отклонени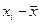й () и (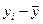), а их знаки («+» или «–»). Коэффициент рассчитывается по следующей формуле:

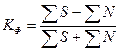, (9.1)

где 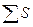– число совпадений знаков;

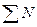– число несовпадений знаков.

Если знаки всех отклонений по каждому признаку совпадут, то 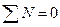и тогда Это характеризует наличие прямой связи. Если все знаки не совпадут, то 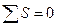и тогда 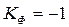, что характеризует обратную связь. Если же 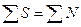, то 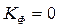. Следовательно, коэффициент Фехнера может принимать значения от 0 до 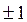. При этом чем ближе значение к 1, тем больше (сильнее) теснота зависимости между рассматриваемыми признаками. Однако, равенство коэффициента Фехнера единице нельзя рассматривать как свидетельство функциональной связи.

Для нашего примера:

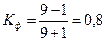
Данное значение характеризует прямую зависимость между изучаемыми признаками.

Следует иметь в виду, что поскольку коэффициент Фехнера зависит только от знаков и не учитывает величину самих отклонений X и Y от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление.