Общее уравнение прямой

Общее уравнение прямой представляется в виде пересечения двух плоскостей:

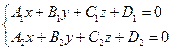(1)

Любой ненулевой вектор параллельный данной прямой, называется направляющим вектором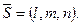

Параметрические уравнения прямой.

М(х,у,z) – произвольная точка прямой, М₀(х₀,у₀,z₀) – данная точка прямой, ненулевой вектор а(m,n,p) – направляющий вектор этой прямой, t – вещественное число (параметр).

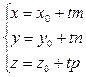(2)

Каноническое уравнение прямой.

Точка М₀(х₀,у₀,z₀) и ненулевой вектор а(m,n,p) – параллелен прямой (называется направляющий вектор).

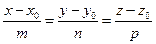(3)

Уравнение прямой, проходящей через две точки.

Пусть даны две точки M₁(x₁; y₁;z₁) и M₂ (x₂; y₂; z₂).

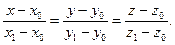(4)