Прямая на плоскости. Взаимное расположение двух прямых. Угол между двумя прямыми. Расстояние от точки до прямой

Угол между двумя прямыми. Условие параллельности

и перпендикулярности двух прямых

Пусть даны две пересекающиеся прямые ; .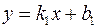

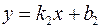Требуется найти острый угол 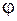между ними.

.

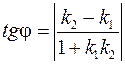Если прямые 1 и 2 заданы их общими уравнениями ; ; ; .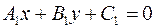

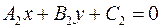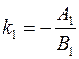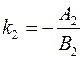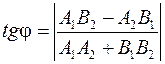
Если прямые - параллельны, то углы 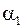и 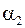равны между собой, то есть .

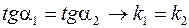Равенство угловых коэффициентов – условие параллельности прямых.

Условие перпендикулярности двух прямых имеет вид: 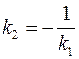или .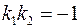

В случае, когда прямые заданы общими уравнениями, условие параллельности 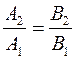; условие перпендикулярности: .

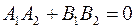Расстояние от точки до прямой

Пусть на плоскости 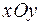задана прямая 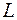своим общим уравнением 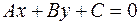и точка 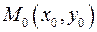. Требуется найти расстояние 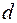от точки 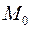до прямой .

: .

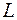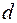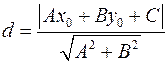Пример: определить расстояние от точки 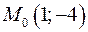до прямой .

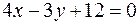Решение: .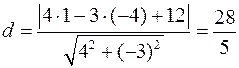

Различные способы задания плоскости.

Общее уравнение плоскости.

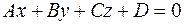. (1)

Параметрические уравнения плоскости.

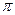- плоскость, 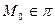, М₀(х₀,y₀,z₀) – точка, 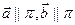, , 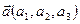, 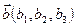а и b не параллельны, u и v – вещественные числа (параметры).

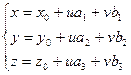(2)

Уравнение плоскости, заданной точкой и двумя неколлинеарными векторами.

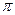- плоскость, 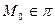, М₀(х₀,y₀,z₀) – точка, 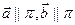, , 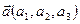, 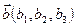а и b не параллельны.

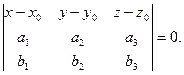(3)

Уравнение плоскости, заданной тремя точками, не лежащими на одной прямой.

- плоскость, , М(х₁,y₁,z₁), М(х₂,y₂,z₂), М(х₃,y₃,z₃) не лежат на одной прямой.

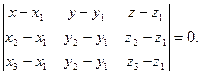(4)

Уравнение плоскости в отрезках.

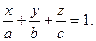(5)

Уравнение плоскости, заданной точкой и вектором нормали

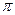- плоскость, 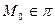, М₀(х₀,y₀,z₀) – точка, 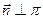, n(A,B,C)

A(x-x₀)+B(y-y₀)+C(z-z₀)=0. (6)

Нормальное уравнение плоскости.

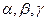- углы, которые составляет перпендикуляр, опущенный из начала координат на плоскость, с осями координат,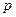- длина перпендикуляра.

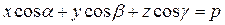. (7)