2014-01-25
2132
Комплексный чертеж точки (Эпюр Монжа)
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
Проецирование геометрического объекта (точки, линии или фигуры) на одну плоскость проекций не определяет его положения в пространстве (какой-либо проекции точки может соответствовать бесчисленное множество точек в пространстве) и не дает полного представления о нем. Поэтому принято использовать не одну, а две или три взаимно перпендикулярные плоскости проекций – горизонтальную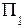 
, фронтальную 
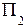и профильную 
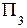. Две плоскости проекций делят пространство на 4 четверти (рис. 2.1 а), три плоскости – на 8 октантов (рис. 2.1 б).
Линии пересечения плоскостей проекций 0x, 0y, 0z называются осями проекций. Они аналогичны осям декартовой системы координат с той разницей, что ось 0x имеет положительное направление влево.
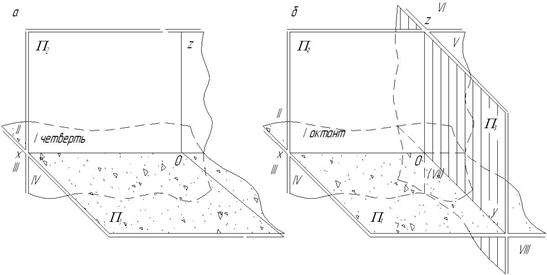
Рис. 2.1
Т.к. любой предмет можно рассматривать как множество точек, проецирование его на плоскость сводится к построению отдельных точек ему принадлежащих. Поэтому все базовые понятия и правила проецирования рассматриваются на примере построения точки.
|
|
|
Построим проекции точки А, расположенной в первом октанте пространства (рис.2.2). Для этого через точку проведем проецирующие лучи, идущие перпендикулярно плоскостям проекций. На пересечении этих лучей с плоскостями проекций находятся проекции самой точки А.
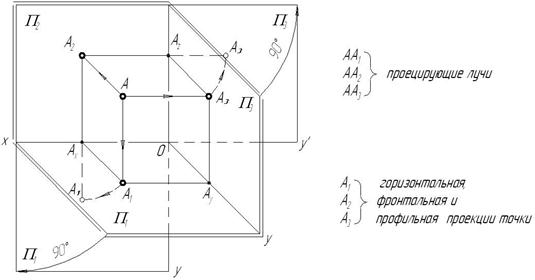
Рис. 2.2
Несмотря на наглядность пространственного изображения, работать с ним неудобно, т.к. горизонтальная и профильная плоскости проекций изображаются на нем с искажением. Удобнее совместить эти плоскости с фронтальной плоскостью проекций, развернув их на угол 90° вокруг осей проекций 0x и 0y. При этом ось 0y разворачивается как с горизонтальной, так и с фронтальной плоскостями проекций, поэтому на чертеже она обозначается дважды – 0y и 0y′.
Полученный таким образом чертеж называется комплексным чертежом (КЧ), или эпюром Монжа. В связи с тем, что он представляет собой развернутую в плоскость пространственную модель, самой точки на комплексном чертеже нет (рис. 2.3).
Проекции точки на КЧ соединяются между собой прямыми линиями, называющимися линиями связи и проходящими перпендикулярно осям проекций.
Независимо от того, в каком октанте находится точка, ее горизонтальная и фронтальная проекции всегда лежат на одной линии связи, перпендикулярной оси 0x, а фронтальная и профильная проекция – на линии связи, перпендикулярной оси 0z.
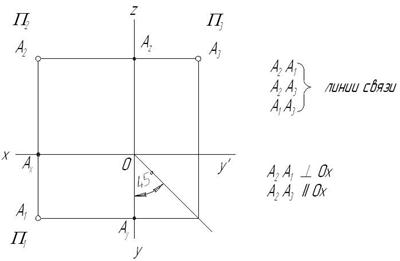
Рис. 2.3
Исходя из рисунка пространственной модели (рис. 2.2) можно выявить взаимосвязь между проекциями точки А:
1) расстояние от точки А до горизонтальной плоскости проекций (высота точки)
|
|
|
;
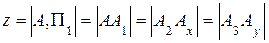2) расстояние от точки А до фронтальной плоскости проекций (глубина точки)
;
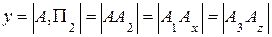3) расстояние от точки А до профильной плоскости проекций (широта точки)
.
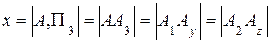Например, расстояние от фронтальной проекции точки до оси 0x равно расстоянию от профильной проекции до оси 0y. Следовательно, по двум любым проекциям точки можно построить третью.
Точки могут занимать частное положение в пространстве относительно плоскостей проекций:
1) если точка расположена на оси проекций, то две ее проекции лежат на этой оси, а третья находится в начале координат;
2) если точка лежит на плоскости проекций, тогда одна из ее проекций лежит в этой плоскости, а две другие – на осях проекций.
Допустим, что точка В лежит на оси 0z, а точка С принадлежит горизонтальной плоскости проекций (рис. 2.4). Для точки С построения следует начинать с проекции, принадлежащей плоскости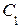 
, для точки В – с проекци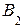й 
и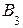 
, лежащих на осях проекций.
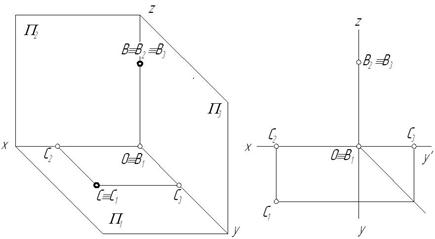
Рис. 2.4
