2015-04-12
1226
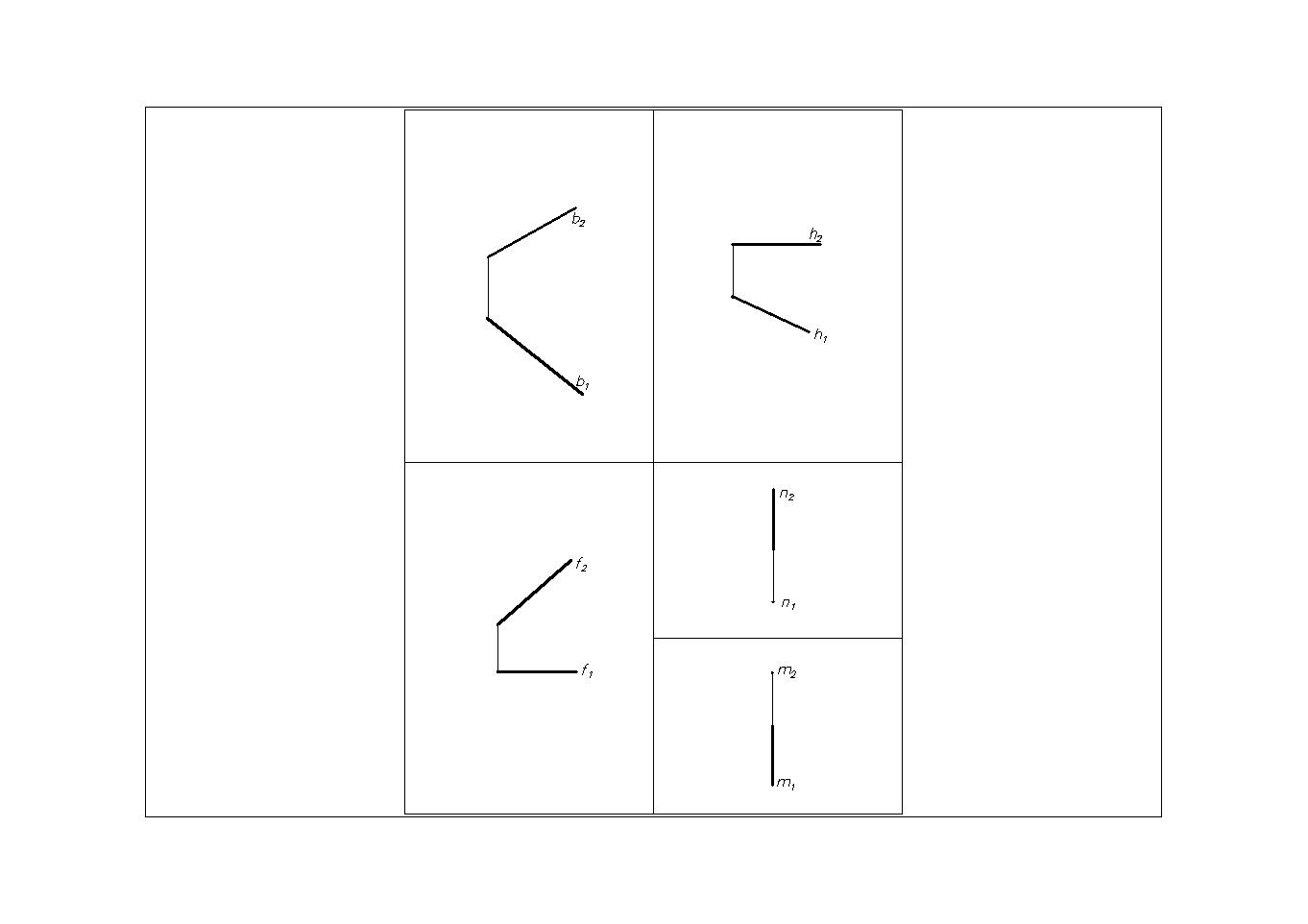
Вышеприведенные чертежи называются однокартинными. Однокартинный чертеж не обладает свойством обратимости. Проекционный чертеж становится обратимым при добавлении дополнительной информации.
| Рис.7 |
| Рис. 6 |
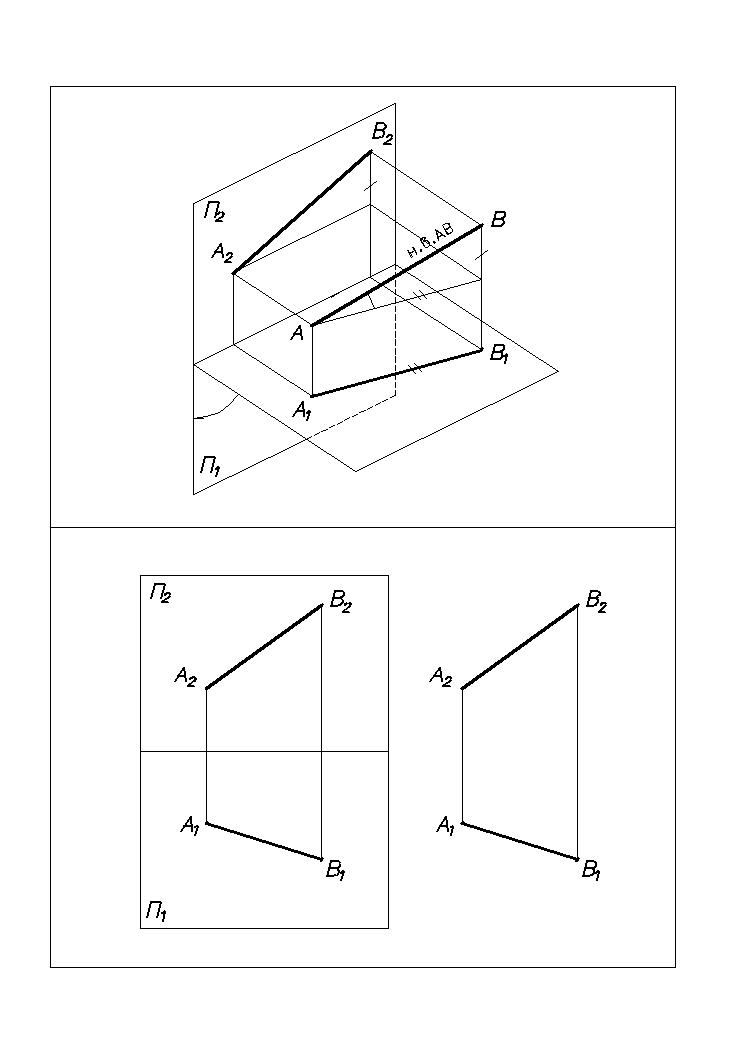
Комплексным чертежом называется чертеж, составленный из двух или более связанных между собой ортогональных проекций изображаемого геометрического образа. Принцип образования: геометрический образ ортогонально проецируется минимум на две взаимно перпендикулярные плоскости проекций, которые затем совмещаются с одной плоскостью. Чертеж на рис. 7 называется комплексным чертежом. А 1 –
горизонтальная проекция точки А; А 2 – фронтальная проекция точки А; А 1 А 2- линия связи. Если на К.Ч. заданы две проекции точки, точка однозначно задана на К.Ч.
На рис. 7 приведен комплексный чертеж прямой АВ. Прямая однозначно задана на комплексном чертеже, если заданы две ее проекции.
Взаимное расположение двух прямых.
| Рис. 8 |
| Рис.10 |
| Рис.9 |
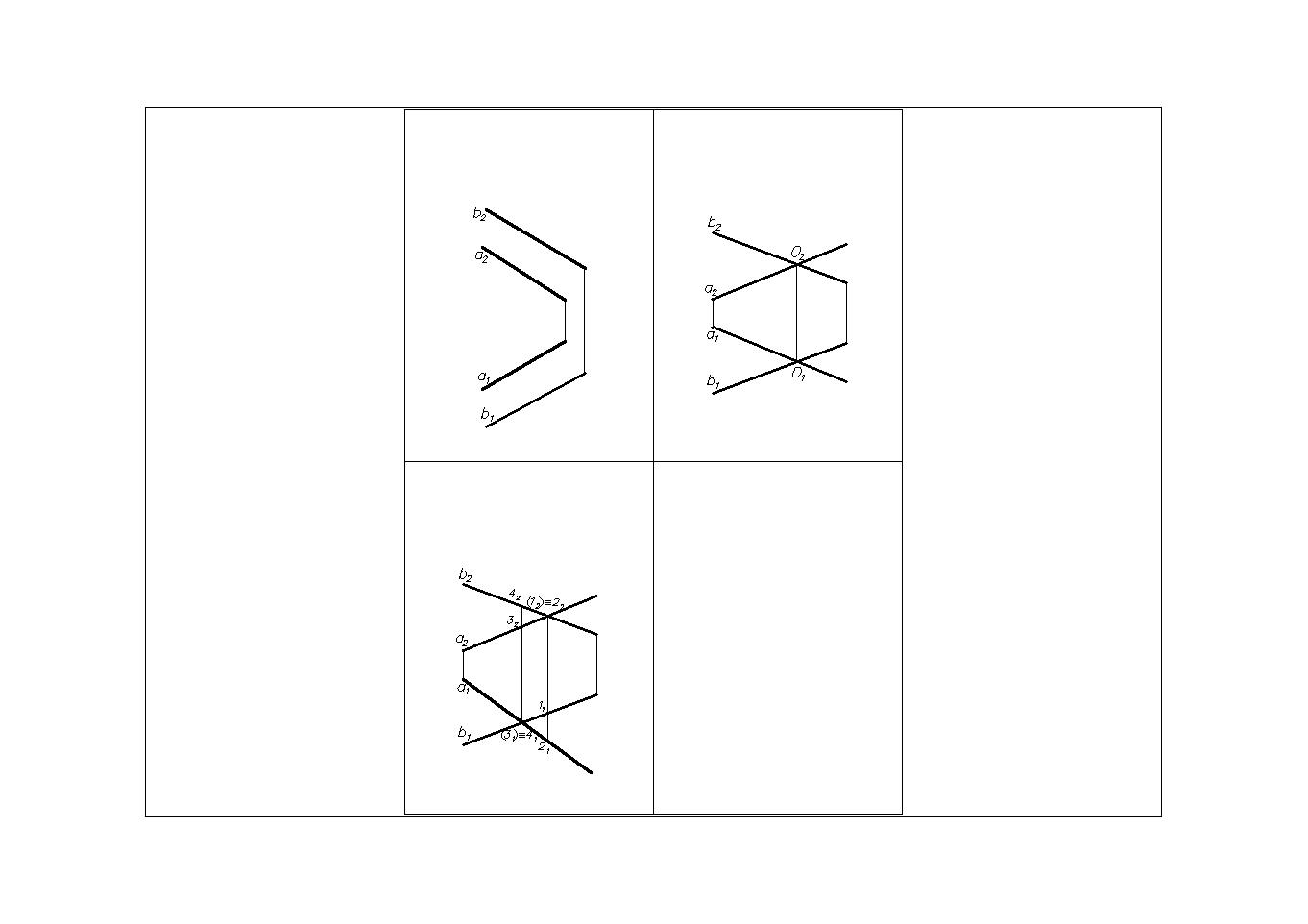
1. Параллельные прямые. Две прямые параллельны между собой, если их одноименные проекции тоже параллельны (Рис.8). Если a II b, то a1 II b1 и a2 II b2.
|
|
|
2. Пересекающиеся прямые (имеют одну общую точку). Две прямые пересекаются между собой, если точки пересечения одноименных проекций прямых лежат на одной линии связи (Рис.9). Если a x b = О, то a 1x b 1 = О 1 и a 2x b 2. = О 2.
3. Скрещивающиеся прямые (не имеют общих точек). Две прямые скрещиваются между собой, если точки пересечения их одноименных проекций лежат на разных линиях связи (Рис.10).
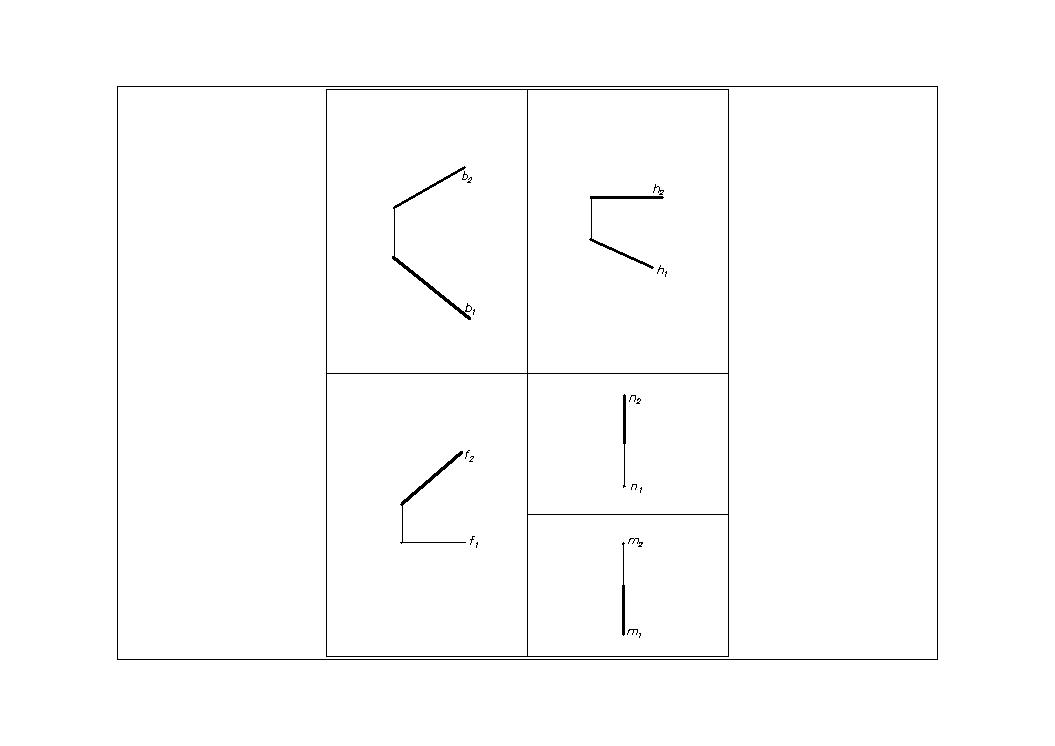Положение прямых линий относительно
плоскостей проекций.
Рис.11 Рис.12 Рис.13 Рис.14
В зависимости от своего положения относительно плоскостей проекций прямые разделяют на прямые общего положения и прямые частного положения.
Прямая общего положения (Рис.11) – прямая, которая имеет углы, отличные от 0 и 90 одновременно со всеми плоскостями проекции (П 1, П 2).
Прямые, которые параллельны плоскостям проекций или перпендикулярные к ним называются прямыми частного положения.
Линии уровня. Горизонталь (Рис. 12) – линия, все точки которой имеют одинаковую координату Z (аппликата). Горизонталь параллельна горизонтальной плоскости проекций. Обозначение горизонтали – h (h II П 1).На П 1: h 1= h, h 1- натуральная величина прямой h.
Фронталь (Рис.13) – линия, все точки которой имеют одинаковую координату Y (ордината). Фронталь параллельна фронтальной плоскости проекций. Обозначение фронтали – f (f II П 2). На П 2 f 2 = f, f 2- натуральная величина отрезка АВ.
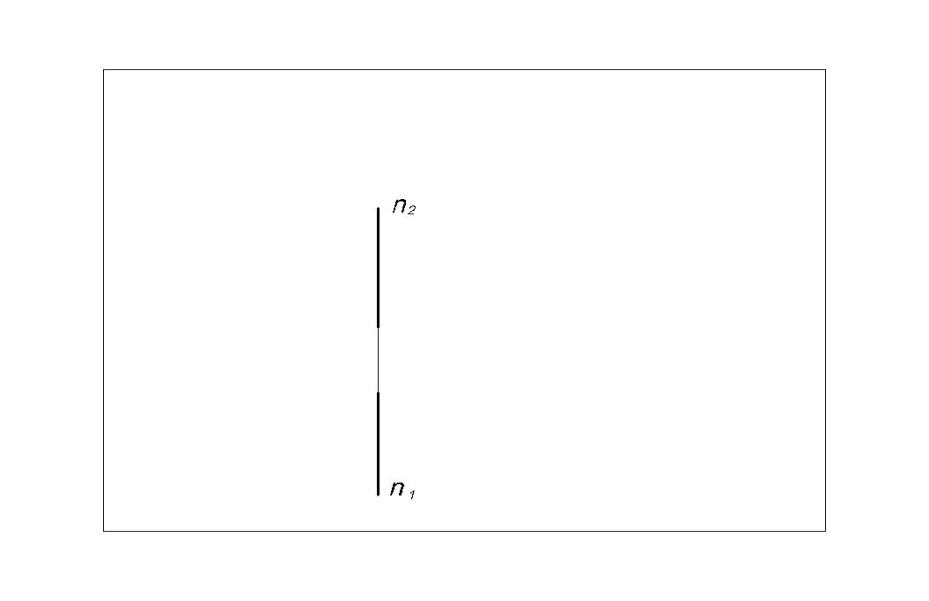
Профильная линия (Рис.14) – линия, все точки которой имеют одинаковую координату X (абсцисса). Профильная линияпараллельна профильной плоскости проекций. Обозначим профильную линию буквой п (п II П 3). На П1 и П 2 проекции профильной линии п совпадают с линией связи.
|
|
|
