Перпендикулярность плоскостей

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

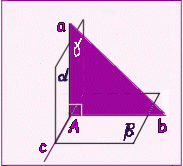• Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
• Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
• Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения
• Если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема.
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ.

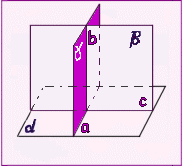Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство:

Пусть 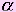- плоскость, b - перпендикулярная ей прямая, 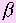- плоскость проходящая через прямую b, и с - прямая по

которой пересекаются плоскост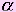и и .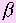

Докажем, что плоскост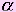и и 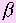перпендикулярны.
Проведем в плоскости 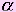через точку пересечения прямой b с плоскостью 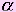прямую а, перпендикулярную прямой с.

Проведем через прямые а и b плоскость 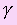. Она перпендикулярна прямой с, так как прямые а и b перпендикулярны, то плоскост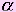и и 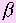перпендикулярны.

Теорема доказана.