Проецирование прямого угла

ПЕРПЕНДИКУЛЯРНОСТЬ ГЕОМЕТРИЧЕКСКИХ ОБЪЕКТОВ

Лекция 5

В общем случае плоский угол проецируется на плоскость проекций с искажением.

Возьмем две прямые общего положения l и k. Прямая l пересекает горизонтальную плоскость проекций под углом a, а прямая k – под углом a¢. Между собой прямые пересекаются под произвольным углом j. Прямоугольная проекция угла j₁ определяется по формуле:

.

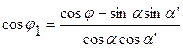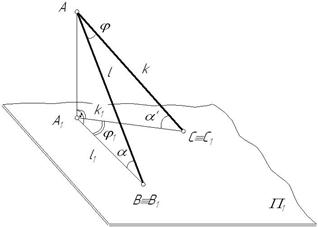
Рис. 4.1

Пусть 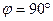, , 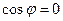тогда при .

.

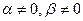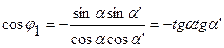При 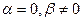, , 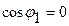следовательно, .

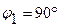Теорема о проецировании прямого угла:

Прямой угол на плоскость проекций проецируется без искажения, если, по крайней мере, один из его лучей параллелен этой плоскости проекций.

Пусть прямые l(АВ) и k(АС) пересекаются под прямым углом. Прямая l параллельна горизонтальной плоскости проекций. Тогда:

1. .

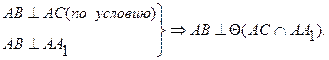
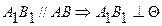2. .

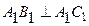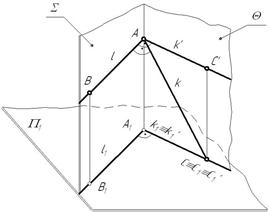
Рис. 4.2

Все прямые, лежащие в плоскости 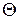, на горизонтальную плоскость проекций проецируются перпендикулярно следу плоскости .

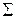Пример: Построить перпендикуляр из точки А к горизонтали.

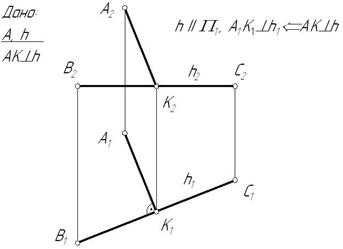
Рис. 4.3