Пересечение прямой с плоскостью

Прямая называется пересекающей плоскость, если она имеет с ней только одну общую точку. Рассмотрим различные случаи пересечения прямой и плоскости.

Частные случаи:

Пример 1. Прямая – проецирующая, плоскость – частного положения.

На КЧ необходимо построить проекции точки пересечения прямой с плоскостью и определить видимость этой прямой относительно горизонтальной и фронтальной плоскостей проекций.

Точка К должна одновременно принадлежать и прямой, и плоскости.

1) Горизонтальную проекцию точки пересечения находим из условия принадлежности ее прямой i. Так как все точки, лежащие на горизонтально-проецирующей прямой, совпадают с ее следом: К₁ º i₁.

2) Определение фронтальной проекции точки пересечения сводится к задаче на принадлежность точки К плоскости :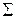

.

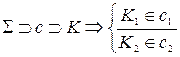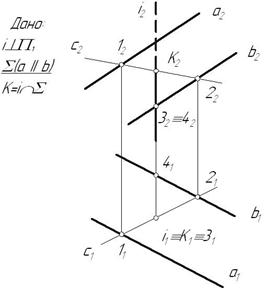
Рис. 3.18

Пример 2. Прямая – общего положения, плоскость – проецирующая.

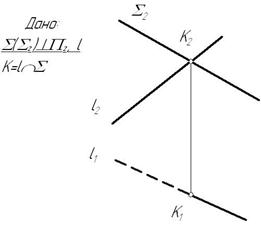
Рис. 3.19

В данном случае фронтальная проекция точки пересечения лежит на следе плоскости

.

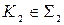Построение недостающей горизонтальной проекции точки пересечения сводится к задаче на принадлежность точки прямой:

.

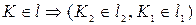Общий случай:

Пересечение прямой общего положения с плоскостью общего положения (первая основная позиционная задача).

В общем случае задача на пересечение прямой с плоскостью решается с помощью вспомогательной секущей плоскости, на которую накладывается ряд условий:

1) она должна быть плоскостью частного положения;

2) должна проходить через заданную прямую

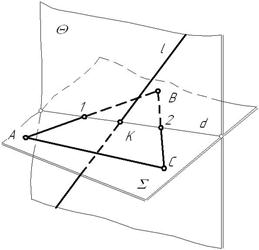
Рис. 3.20

Порядок нахождения точки пересечения прямой с плоскостью:

1) Через прямую l проводится вспомогательная плоскость частного положения .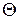

2) Определяется линия пересечения вспомогательной плоскости 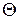с заданной плоскостью .

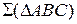3) На пересечении линии пересечения плоскостей 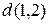с заданной прямой находится точка К, являющаяся искомой точкой.

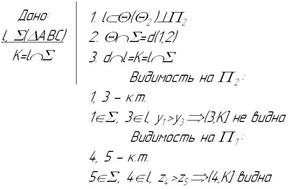
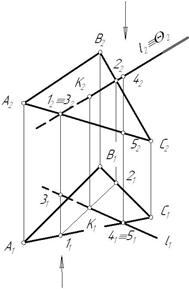
Рис. 3.21