Пересечение многогранников

Пересечение поверхностей

Многогранники пересекаются по замкнутым пространственным ломаным линиям, которые могут быть найдены следующим образом:

1. Способ ребер. Находятся точки пересечения ребер одного многогранника с гранями другого.

2. Способ граней. Определяются отрезки прямых, по которым грани одного многогранника пересекаются с гранями другого.

Пример: Построить линию пересечения двух трехгранных призм, одна из которых проецирующая.

В результате пересечения заданных многогранников получается ломаная пространственная линии. Она соединяет соответствующие точки пересечения ребер одного многогранника с гранями другого. Так как одна из призм проецирующая относительно горизонтальной плоскости проекций, горизонтальная проекция линии пересечения совпадает с горизонтальным очерком этой призмы. Искомые точки сечения можно получить, решая задачу на пересечение прямой (ребра) с плоскостью (гранью).

, .

, .

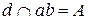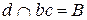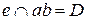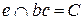Для построения точек пересечения ребра b с гранями призмы, используется горизонтально-проецирующая плоскость .

.

.

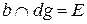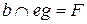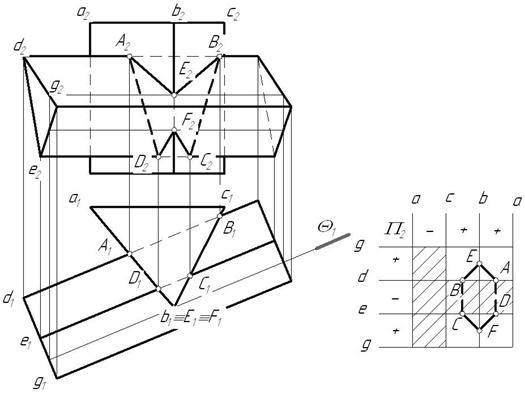
Рис. 6.18

Для определения видимости линии сечения строится диаграмма, на которой схематично в произвольных размерах изображаются грани заданных призм. Знаками ²+² и ²-² отмечается видимость граней многогранников. На соответствующих гранях и ребрах наносятся точки сечения, и соединяют их с учетом видимости. Видимыми считаются те звенья линии пересечения, которые лежат на видимых гранях обоих многогранников.