Метод координат

ВВЕДЕНИЕ

ОГЛАВЛЕНИЕ

ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ

Краткий конспект лекций по аналитической геометрии предназначен для самостоятельной работы студентов очной, очно-заочной и заочной форм обучения по дисциплине «Алгебра и геометрия». Содержит теоретический материал, примеры решения и контрольные вопросы по данному разделу высшей математики.

Введение
Лекция 1. Метод координат
Лекция 2. Прямые на плоскости
Лекция 3. Прямые в пространстве
Лекция 4. Плоскости в пространстве
Лекция 5. Кривые второго порядка
Контрольные вопросы

Краткий конспект лекций по аналитической геометрии предназначен для самостоятельной работы студентов очной, очно-заочной и заочной форм обучения по дисциплине «Алгебра и геометрия». Содержит теоретический материал, примеры решения и контрольные вопросы по данному разделу высшей математики.

Лекция 1

Контрольные вопросы:

1. Расстояние между двумя точкам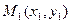и и 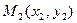на плоскости.

2. Нахождение координат 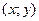точки М, делящей в отношении λ заданный отрезок.

3. Нахождение площади треугольника по координатам его вершин.

Метод координат заключается в установлении соответствия между точками прямой (плоскости, пространства) и их координатами – действительными числами при помощи системы координат.

Прямоугольная система координат Оху на плоскости задается двумя взаимно перпендикулярными прямыми, на каждой из которых выбрано положительное направление и задан единичный отрезок.

Координатами точки М в системе координат Оху называются координаты радиус-вектора .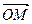

Расстояние между двумя точкам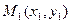и и 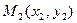на плоскости вычисляется по формуле

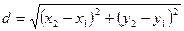. (1)

Координаты 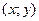точки М, делящей в заданном отношении λ отрезок АВ, где 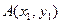, , 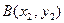, 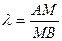находятся по формулам

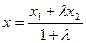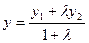, . (2)

Если λ = 1, т.е. точка М делит отрезок АВ пополам, получаются формулы координат середины отрезка

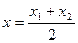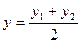, . (3)

Площадь треугольника с вершинами 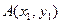, , 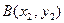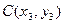вычисляется по формуле

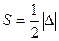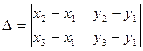, где . (4)

Пример 1. Отрезок AB четырьмя точками разделён на пять равных частей. Определить координату ближайшей к A точки деления, если A(-3), B(7).