1. Теорема сложения вероятностей несовместных событий.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Доказательство: пусть n -общее число возможных элементарных исходов опыта, m -число исходов, благоприятствующих событию A, k -число исходов, благоприятствующих событию B. Изобразим наглядно схему случая.
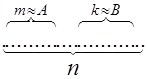
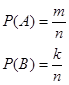 ,
,
Т.к. события A и B несовместны, то нет таких исходов, которые благоприятствуют и A и B вместе.
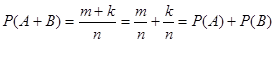
Поэтому число исходов, благоприятствующие событию A+B=m+k.
Замечание: для любого числа попарно несовместных событий, теорема формируется аналогично.
Пример.
При стрельбе вероятность сделать отличный выстрел 0,3; хорошо-0,4, какова вероятность сделать выстрел не ниже хорошо? Обозначим A -отлично, B -хорошо, C -полученные оценки не ниже хорошо, тогда C=A+B, причем A и B несовместны. По теореме C =0,4+0,3=0,7.
Рассмотренная теорема сложения применима только к несовместным событиям. Это положение очень важно; без него теорема сложения становится неверной, и применение ее приводит к грубым ошибкам.
Например: Пусть два стрелка стреляют в цель одновременно, причем для первого стрелка вероятность попадания в цель равна 0,8, а для второго-0,7. Какова вероятность поражения цели?
Если к решению этой задачи применить рассмотренную выше теорему сложения, то найдем, что искомая вероятность равна 0,8+0,7=1,5- результат явно нелепый, т.к. знаем, что вероятность события не может быть больше 1. К этому неверному ответу пришли потому, что применили теорему к такому случаю, в котором рассматриваются совместные события. Ибо вполне возможно, что оба стрелка поразят цель при одном и том же двойном выстреле.
Теорема сложения вероятностей в общем случае: вероятность суммы событий равна сумме вероятностей минус вероятность произведения этих событий.
P(A+B)=P(A)+P(B)-P(A×B)
Доказательство:
Пусть имеется n -исходов, которые благоприятствуют событию A, k -событию B, l -исходов событию AB, сумме благоприятствуют (m+k)-l
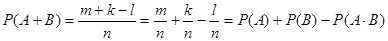
Если A и B несовместные события, то P(A×B)= 0
 2014-01-25
2014-01-25 747
747







