2014-01-25
1173
Следствием обеих основных теорем - теоремы сложения вероятностей и теоремы умножения вероятностей- являются так называемая формула полной вероятности.
Пусть событие A может появиться лишь с одним из несовместных событий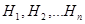 
, 
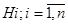, которое образует полную группу. Сначала появляется одно из событий 
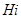, а затем событие A, которое при этом может появиться или не появиться.
Пусть известны вероятности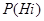 
и условные вероятности события 
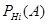, какова будет при этом вероятность появления события A? Появление события A означает осуществление одного, безразлично какого из несовместных событий
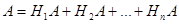
Следовательно, событие A- есть сумма этих событий, т.к. если Hi несовместно, то их комбинация HiA также несовместна. По теореме сложения вероятность события
.
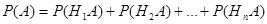По теореме умножения вероятностей.
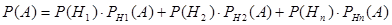
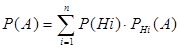- формула полной вероятности.
Вероятность события A равна сумме произведений каждого из несовместных событий 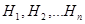, на соответствующую условную вероятность события A. Т.к. событие A образует полную группу, то 
.
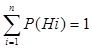Т.к. заранее неизвестно, какое событие раньше наступит, то эти события называются гипотезами.
|
|
|
Пример: При разрыве снаряда образуются крупные, средние и мелкие осколки, причем число крупных осколков составляет 0,1 их общего числа, а число средних и мелких - соответственно 0,3 и 0,6 общего числа осколков. При попадании в танк крупный осколок пробивает броню с вероятностью 0,9, средний- с вероятностью 0,3 и мелкий - с вероятностью 0,1. Какова вероятность того, что попавший в броню осколок пробьет ее?
Решение:
В данном примере 3 гипотезы, вероятности которых P(H 1 ) =0,1; P (H 2)=0,3 и P (H 3)=0,6.
Событие A - попадание осколка в броню. Пользуясь формулой полной вероятности, находим:
P (A)=0,1×0,9+0,3×0,3+0,6×0,1=0,24
