Случайное событие. Вероятность

Теория вероятностей

Лекции по биофизике

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Антонов В.Ф. с соавт.. “Биофизика”. – М., Владос, 1999,288с.

2. Бергельсон А.А. Мембраны, молекулы, клетки. М., Наука, 1982.

3. Болдырев А. А. Введение в биомембранологию. М., Высшая школа, 1990.

4. Владимиров Ю.А. с соавт. Биофизика. М., Медицина, 1983.

5. Губанов Н.И., Утепбергенов А.А. Медицинская биофизика. М., Медицина, 1978.

6. Корнеев Ю.А., Коршунов А.П., Погадаев В. Медицинская и биологическая физика. – М: Медицинская книга; Новгород: Изд-во НГМА, 2001. – 250 с.

7. Костюк П.Г. с соавт. Биофизика. Киев, 1988,504 с.

8. Ремизов А.Н. Медицинская и биологическая физика. М. «Высшая школа, 1996.

9. Ремизов А.И. Медицинская и биологическая физика: Учебник для вузов. – М.: Дрофа, 2003. – 560 с.

10. Рощупкин Д.И., Артюхов В.Г. Основы фотобиофизики. Воронеж, 1997.

11. Рощупкин Д.И., Фесенко Е.Е., Новоселов В.И. Биофизика органов. Учеб.пособие.-М:Наука,2000.-255с.

12. Рубин А.Е. Биофизика.1-2 том. М.Высшая школа,1987.

13. Рыбин Н.И. Лекции по биофизике. Свердловск. СГУ,1990,240 с.

14. Сомьен Дж. Кодирование сенсорной информации М.,Мир, 1975.

15. Тарусов Б.Н., Колье О.Р. Биофизика, М.Высшая школа,1968,500с.

16. Физиология кровообращения. Физиология сердца. Л., Наука, 1980.

17. Физиология дыхания. Л, Наука, 1973.

Учебно-методическое пособие

Под редакцией проф. Баскакова М.Б.

И.В.Ковалев, И.В.Петрова, Л.В.Капилевич

Макет издания подготовлен в
Центре дистанционного образования СибГМУ

Отпечатано в лаборатории оперативной полиграфии СибГМУ
Заказ №___Тираж_____экз.

В теории вероятностей исследуются закономерности, относя­щиеся к случайным событиям, величинам, процессам. Врачи редко задумываются, что постановка диагноза имеет вероятно­стный характер и, как остроумно замечено, лишь патологоанатомическое исследование может достоверно определить ди­агноз умершего человека.

Наблюдая различные явления, можно заметить, что существу­ет два типа связей между условиями S и наступлением или ненас­туплением некоторого события А. В одних случаях осуществление комплекса условий S (испытание) непременно вызывает событие А. Так, например, материальная точка массой т₀ под воздействи­ем силы F (условие S) приобретает ускорение а = F/m₀ (событие А). В других случаях многократное повторение испытания может привести или не привести к появлению события А. Такие события принято называть случайными: к ним можно отнести появление в кабинете врача больного с данной болезнью, выпадение опреде­ленной стороны монеты при ее бросании и др.

Не следует думать о случайных явлениях как о беспричинных, ничем не обусловленных. Известно, что многие явления связаны между собой, отдельное явление представляет следствие како­го-то другого и само служит причиной последующего. Однако проследить количественно эту связь между условиями и событи­ем часто затруднительно или даже невозможно. Так, при броса­нии игральной кости (однородный кубик с пронумерованными шестью гранями: 1, 2, 3, 4, 5 и 6) окончательное положение куби­ка зависит от движения руки в момент бросания, сопротивления воздуха, положения кубика при попадании на поверхность, осо­бенности поверхности, на которую упал кубик, и других факто­ров, которые в отдельности учесть невозможно.

В быту применительно к таким случайным событиям употреб­ляют слова «возможно», «вероятно», «маловероятно», «невероятно». В некоторых случаях такая оценка больше характеризует желание говорящего, чем истинную степень возможности или не­возможности события. Однако и случайные события, если их чис­ло достаточно велико, подчиняются определенным закономернос­тям. Количественная оценка закономерностей, относящихся к случайным событиям, дается в разделе математики, называемом теорией вероятностей.

Теория вероятностей изучает закономерности, присущие мас­совым (статистическим) случайным событиям.

Отдельные исторические факты, «неожиданности», «катастро­фы» являются единичными, как бы неповторимыми, событиями, и количественные вероятностные суждения относительно них сделать невозможно. Исторически теория вероятностей появи­лась в связи с попытками подсчета возможности различных исхо­дов в азартных играх. В настоящее же время она применяется в науке, в том числе биологии и медицине, для оценки вероятности практически важных событий. От игр остались лишь наглядные примеры, которые удобно использовать для иллюстрации теоре­тических положений.

Статистическое определение вероятности. Вероятность Р(А) в теории вероятностей выступает как числовая характеристика сте­пени возможности появления какого-либо определенного случай­ного события А при многократном повторении испытаний.

Допустим, при 1000 бросаний игральной кости цифра 4 выпа­дает 160 раз. Отношение 160/1000 = 0,16 показывает относитель­ную частоту выпадания цифры 4 в данной серии испытаний. В бо­лее общем случае, когда случайное событие А происходит т раз в серии п независимых испытаний, относительной частотой со­бытия в данной серии испытаний или просто частотой события А называют отношение

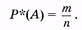(2.1)

При большом числе испытаний частота события примерно по­стоянна: увеличение числа испытаний уменьшает колебание час­тоты события около постоянной величины.

Вероятностью случайного события назовем предел, к ко­торому стремится частота события при неограниченном увеличении числа испытаний:

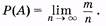(2.2)

Естественно, что никто и никогда не сможет проделать неогра­ниченное число испытаний для того, чтобы определить вероят­ность. В этом нет и надобности. Практически за вероятность [см. (2.2)] можно принять относительную частоту события при боль­шом числе испытаний. Так, например, из статистических законо­мерностей рождения, установленных за много лет наблюдений, вероятность того события, что новорожденный будет мальчиком, оценивают в 0,515.

Классическое определение вероятности. Если при испыта­ниях нет каких-либо причин, вследствие которых одно случайное событие появлялось бы чаще других (равновозможные собы­тия), можно определить вероятность исходя из теоретических со­ображений. Например, выясним в случае бросания монеты часто­ту выпадания герба (событие А). Разными экспериментаторами при нескольких тысячах испытаний было показано, что относи­тельная частота такого события принимает значения, близкие к 0,5. Учитывая, что появление герба и противоположной стороны монеты (событие В) являются событиями равновозможными, ес­ли монета симметрична, суждение Р(А) = Р(В) = 0,5 можно было бы сделать и без определения частоты этих событий. На основе по­нятия «равновозможности» событий формулируется другое опре­деление вероятности.

Допустим, что в результате испытания должно произойти только одно из п равновозможных несовместных событий (несов­местными называют события, если их одновременное осуществ­ление невозможно). Пусть рассматриваемое событие А происхо­дит в т случаях, которые называются благоприятствующими А, и не происходит при остальных п - т, неблагоприятствующих А. Тогда вероятностью можно назвать отношение благоприят­ствующих случаев к общему числу равновозможных несов­местных событий:

Р(А) = m/n. (2.3)

Это классическое определение вероятности.

Рассмотрим не­сколько примеров.

1. В урне находится 40 шаров: 10 черных и 30 белых. Найти вероят­ность того, что вынутый наугад один шар будет черным.

Число благоприятствующих случаев равно числу черных шаров в урне: т = 10. Общее число равновозможных событий (вынимание одного шара) равно полному числу шаров в урне: п = 40. Эти события несовмест­ны, так как вынимается один и только один шар. По формуле (2.3) имеем:

Р(А) = 10/40 = 1/4.

2. Найти вероятность выпадания четного числа при бросании играль­ной кости.

При бросании кости реализуются шесть равновозможных несов­местных событий: появление одной цифры 1, 2, 3, 4, 5 или 6, т. е. п = 6. Благоприятствующими случаями являются выпадания одной из цифр 2, 4 или 6: т = 3. Искомая вероятность:

Р(А) = m/n – 3/6 = 1/2.

Как видно из определений вероятности события (2.2) и (2.3), для всех событий 0 £ Р(А) £ 1.

События, которые при данных испытаниях не могут про­изойти, называются невозможными: их вероятность равна нулю.

Так, например, невозможно из урны с белыми и черными ша­рами вытащить красный шар, невозможно на игральной кости получить цифру 7.

Событие, которое при данном испытании обязательно произойдет, называется достоверным, его вероятность рав­на 1.

Примером достоверного события является извлечение белого шара из урны, в которой находятся только белые шары.

В ряде случаев вычислить вероятность события оказывается проще, если представить его в виде комбинации более простых со­бытий. Этой цели служат некоторые теоремы теории вероятнос­тей.

Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несов­местных событий равна сумме их вероятностей. Для двух несовместных событий

Р(А или В) = Р(А) + Р(В). (2.4)

Докажем эту теорему. Пусть п — общее число испытаний, т₁ — число случаев, благоприятствующих событию А, т₂ — число слу­чаев, благоприятствующих событию В. Число случаев, благопри­ятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Тогда Р(А или В) = (т₁ + т₂)/п = т₁/п + т₂/п. Отсюда, учитывая (2.3), имеем

Р(А или В) = Р(А) + Р(В).

* Найти вероятность выпадания 1 или 6 при бросании игральной кости.

События А (выпадание 1) и В ( выпадание 6) являются равновозможными: Р(А) = Р(В) = 1/6, поэтому из (2.4) находим Р(А или В) =1/6 + 1/6 = 1/3.

Сложение вероятностей справедливо не только для двух, но и для любого числа несовместных событий.

* В урне находится 50 шаров: 10 белых, 20 черных, 5 красных и 15 си­них. Найти вероятность появления белого, или черного, или красного шара при однократной операции изъятия шара из урны.

Вероятность вынимания белого шара (событие А) равна Р(А) = 10/50 = 1/5, черного шара (событие В) — Р(В) = 20/50 = 2/5 и крас­ного (событие С) — Р(С) = 5/50 = 1/10. Отсюда по формуле сложения ве­роятностей получим Р(А или В или С) = Р(А) + Р(В) + Р(С) = 1/5 + 2/5 + + 1/10= 7/10.