Пример. Статистическое определение вероятности

Задача 3.

Задача 2.

Задача 1.

Статистическое определение вероятности.

Под статистической вероятностью понимают относительную частоту появления события А в n произведенных опытах, т.е.

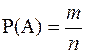, где n – число произведенных опытов, m – число появлений события А.

Рассмотрим задачи на вычисление вероятностей случайных событий с помощью классического определения.

Каков вероятность того, что при бросании монеты выпадет «орел»?

Решение. Обозначим событие А – выпадение «орла». Определим чему равны n и m. В данном случае возможны два элементарных исхода («орел», «решка»), следовательно, n = 2. «Орел» на монете только один, следовательно, m = 1. Получаем, что P(A) = 1/2.

Ответ: вероятность того, что при бросании монеты выпадет «орел» равна 1/2.

Какова вероятность того, что при бросании игрального кубика выпадет число очков, делящееся на 3?

Решение. Обозначим событие А – выпадение числа очков, делящегося на 3. Так как на 3 делятся 3 и 6, то m = 2; n = 6, так как всего 6 элементарных исходов опыта. Отсюда, P(A) = 2/6 = 1/3.

Ответ: вероятность того, что при бросании игрального кубика выпадет число очков, делящееся на 3, равна 1/3.

В ящике находится 5 белых, 6 зеленых и 5 красных шара. Какова вероятность вытащить наугад а) белы шар; б) 2 зеленых шара; в) 3 белых, 4 зеленых и 1 красный шар?

Решение:

а) пусть А – вытащили белый шар. Общее количество элементарных событий n = 5 + 6 + 4 = 15 (общее количество шаров). Количество элементарных событий, благоприятствующих А, m = 5 (количество белых шаров). Отсюда, P(A) = 5/15 = 1/3;

б) пусть В – вынули 2 зеленых шара. Общее количество элементарных событий – это количество способов, которыми можно достать 2 шара из имеющихся, т.е. 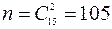. Количество благоприятствующих элементарных событий – это число способов достать 2 зеленых шара из имеющихся зеленых шаров, т.е. 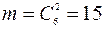. Отсюда, P(A) = 15/105 = 1/7;

в) пусть С – вытащили 3 белых, 4 зеленых и 1 красный шар. Общее количество элементарных событий – это сколькими способами можно достать 3+4+1=8 шаров из имеющихся 15, т.е. 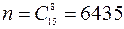. Количество благоприятствующих элементарных событий – это число способов достать 3 белых шара из имеющихся 5 белых, 4 зеленых – из 6 зеленых и 1 красный – из 4 красных шаров, т.е. 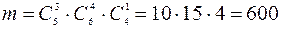(использовали принцип умножения комбинаторики). Получаем, что P(C) = 600/6435 = 0,09.

Ответ: а) вероятность равна 1/3; б) вероятность равна 1/7; в) вероятность равна 0,09.

§ 3. Теоремы сложения и произведения вероятностей

Введем понятия, позволяющие выразить одни события через другие.

Суммой двух событий А и В в данном опыте называется событие С, состоящие в появлении хотя бы одного из событий А и В. Обозначение: C = A + B.

Произведением двух событий А и В в данном опыте называется событие С, состоящие в совместном появлении и события А, и события В. Обозначение: С = AB.

Понятия суммы и произведения могут быть распространены на случай любого конечного числа событий. Суммой нескольких событий называется событие, состоящие в появлении хотя бы одного из этих событий. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Пример.

Бросают игральный кубик. Пусть А₁ – выпало 2 очка, А₂ – выпало 4 очка, А₃ – выпало 6 очков. Тогда событие А – выпало четное число очков является суммой событий А₁, А₂, А₃, т.е. А = А₁ + А₂ + А₃.

Пусть В – выпало не более двух оков. Тогда выпадение двух очков можно представить как произведение двух событий А и В, т.е. А₁ = АВ.

Вспомним определение несовместных событий. События несовместны, если появление одного из них исключает появление другого в одном и том же опыте. Отсюда получаем, что произведение несовместных событий – пустое множество.

Рассмотрим следующие теоремы сложения вероятностей.

ТЕОРЕМА 1. Для любых событий А и В вероятность их суммы находится по формуле

Р(А+В) = Р(А) + Р(В) – Р(АВ)

Если события А и В несовместны, то

Р(А+В) = Р(А) + Р(В).

ТЕОРЕМА 2. Вероятность суммы нескольких несовместных событий равна

Р (А₁+А₂+…+А_n) = Р (А₁) + Р (А₂)+…+Р (А_n).

ТЕОРЕМА 3. Сумма вероятностей событий, образующих полную группу равна единице, т.е.

Р(А₁) + Р(А₂) +…+ Р(А_n) = 1,

если А₁, А₂,…,А_n образуют полную группу событий.

Введем еще одно необходимое нам понятие. События А и В называются независимыми, если появление или не появление одного из них не изменяет вероятности наступления другого. В противном случае события называются зависимыми.

Пусть А — выигрыш по первому лотерейному билету, В — выигрыш по второму билету. События А и В независимы, т.к. выигрыш по одному билету не изменит вероятности выигрыша по другому.

В случае зависимых событий возникает понятие условной вероятности. Условной вероятностью события А по событию В называется вероятность события А, вычисленная при условии, что событие В произошло. Условная вероятность события А по событию В обозначается Р_B(А).

Сформулируем теперь теоремы о произведении вероятностей.

ТЕОРЕМА 4. Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого, при условии, что первое событие наступило, т.е.

Р(АВ) = Р(А)Р_B(В) или Р(АВ) = Р(В)Р_B(А)

ТЕОРЕМА 5. Вероятность произведения двух независимых событий равна произведению их вероятностей, т.е.

Р(АВ) = Р(А)Р(В)

ТЕОРЕМА 6. Вероятность произведения нескольких независимых событий равна произведению их вероятностей, т.е.

Р(A₁A ₂...А_n) = Р(А₁)Р(А₂)...Р(A_n)

ТЕОРЕМА 7. Вероятность произведения нескольких зависимых событий находится по формуле

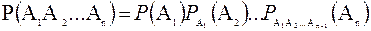
Рассмотрим задачи.