Формула сложения n событий
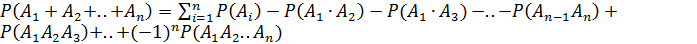
Пусть некоторое событие А может наступить или не наступить с одним из ряда несовместных событий 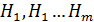 , составляющих полную группу. События такого рода обычно называют гипотезами. Известно также условные вероятности наступления события А при составлении каждой из указанных гипотез.
, составляющих полную группу. События такого рода обычно называют гипотезами. Известно также условные вероятности наступления события А при составлении каждой из указанных гипотез.
Вероятность события А определяется по следующей теореме:
Вероятность события А, которое может произойти вместе с одной и гипотез 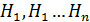 равна сумме парных произведений вероятностей каждой из этих гипотез на отвечающее им условие вероятности наступления события А.
равна сумме парных произведений вероятностей каждой из этих гипотез на отвечающее им условие вероятности наступления события А.
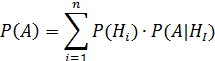
Эта формула носит название функции полной вероятности&
Доказательство:
Т.к. гипотезы 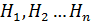 образуют полную группу, то событие А можно представить в виде следующей суммы событий:
образуют полную группу, то событие А можно представить в виде следующей суммы событий:
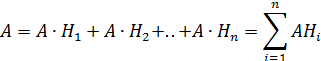
Т.к. события 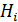 не совместны, то и событие
не совместны, то и событие 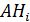 также несовместно. Это позволяет применить для определения вероятности события А теорему сложения вероятностей несовместных событий.
также несовместно. Это позволяет применить для определения вероятности события А теорему сложения вероятностей несовместных событий.
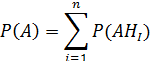
Вероятность произведения находится по аксиоме умножения вероятностей:
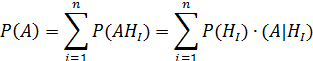
ч.т.д.
Теорема гипотез (формула Бейеса)
До сих пор мы рассматривали вероятности событий до испытаний, т.е. в комплексе условий не фигурировал результат проведения опыта.
Решим следующую задачу: Имеется полная группа несовместных гипотез 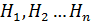 . Известны вероятности каждой из гипотез
. Известны вероятности каждой из гипотез 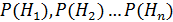 . Производится опыт и в его результате осуществляется некоторое событие А, вероятности которого по каждой из гипотез известны
. Производится опыт и в его результате осуществляется некоторое событие А, вероятности которого по каждой из гипотез известны 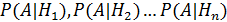 . Найти какие вероятности меют гипотезы
. Найти какие вероятности меют гипотезы 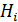 в связи с появлением события А, т.е. найти условные вероятности
в связи с появлением события А, т.е. найти условные вероятности 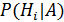 .
.
Теорема гипотез:
Верояность гиопотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события:
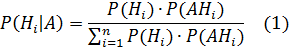
Доказательство:
На основании аксиомы умножения вероятностей
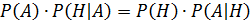
Разрешая это уравнение относительно 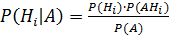 .
.
Выражая P(A) получим (1) ч.т.д.
Если все гипотезы 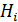 до испытания имеют одинаковую вероятность, т.е.
до испытания имеют одинаковую вероятность, т.е. 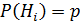 , то формула Бейеса принимает вид:
, то формула Бейеса принимает вид:
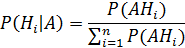
 2014-02-18
2014-02-18 411
411








