Модель авторегрессии 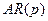 .
.
Основная идея данного метода анализа временного ряда состоит построении линейной модели зависимости 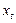 от предыдущих значений временного ряда
от предыдущих значений временного ряда 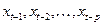 , следующего вида:
, следующего вида:
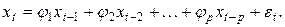 (22)
(22)
Для более простой записи такого рода моделей можно использовать лаговый оператор.
Лагом переменной называется ее значение в предыдущий момент времени:
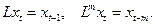 (23)
(23)
Наряду с понятием лаговый оператор существует понятие лаговый многочлен:
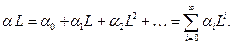 (24)
(24)
С использованием (24) формулу (22) можно переписать следующим образом:
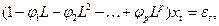 (25)
(25)
где 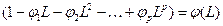 - оператор авторегрессии, и модель (22) можно переписать более кратко:
- оператор авторегрессии, и модель (22) можно переписать более кратко:
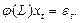 (26)
(26)
Модель процесса Маркова 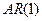 записывается следующим образом:
записывается следующим образом:
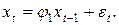 (27)
(27)
Свойства данного процесса: 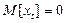 ,
, 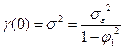 , если
, если 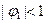 . В случае, если
. В случае, если 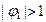 ,
, 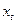 неограниченно растет и дисперсия процесса будет стремиться к
неограниченно растет и дисперсия процесса будет стремиться к 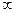 .
.
Коэффициент автоковариации между 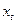 и
и 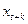 равен
равен 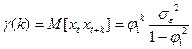 .
.
Соответственно, коэффициент автокорреляции равен 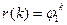 .
.
Условие стационарности процесса: 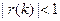 или
или 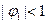 .
.
Примеры процессов авторегрессии первого порядка приводятся на следующих графиках
Модель процесса Юла 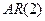 записывается следующим образом:
записывается следующим образом:
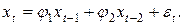 (28)
(28)
Условие стационарности для данного процесса: корни уравнения
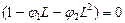 должны лежать вне единичного круга
должны лежать вне единичного круга 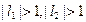 .
.
Коэффициенты модели вычисляются следующим
образом: 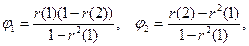
при условии 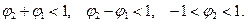
Общая модель 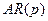 .
.
Для модели вида:
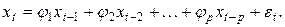 (29)
(29)
коэффициенты определяются следующим образом.
Умножим уравнение (29) на 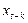 и вычислим математические ожидания правой и левой части уравнения:
и вычислим математические ожидания правой и левой части уравнения:
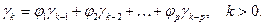
Делением на 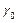 правой и левой частей уравнений, получаем рекуррентное соотношение:
правой и левой частей уравнений, получаем рекуррентное соотношение:
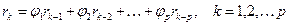 . (30)
. (30)
На основании формулы (30) строится система уравнений Юла-Уокера:
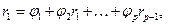
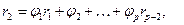
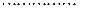
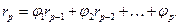
Кроме непосредственного решения системы Юла-Уокера, на практике коэффициенты модели определяются также по методу наименьших квадратов.
Модель скользящего среднего 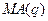 .
.
Основная идея данного метода анализа временного ряда состоит в построении линейной модели зависимости 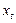 от предыдущих ошибок
от предыдущих ошибок 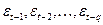 , следующего вида:
, следующего вида:
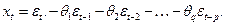 (31)
(31)
При помощи лагового оператора можно привести модель (31) к виду: 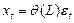 , где
, где 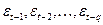 - инновации, белый шум.
- инновации, белый шум.
На основании свойств белого шума 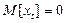 ,
, 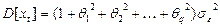 . Эти условия означают, что процесс, представленный моделью (31), стационарный.
. Эти условия означают, что процесс, представленный моделью (31), стационарный.
Коэффициент автокорреляция вычисляется следующим образом:
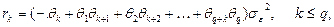
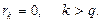
Любую модель MA можно привести к модели AR, это свойство меделей получило название свойство обратимости. Рассмотрим модель 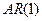 :
:
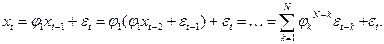
При  в правой части уравнения содержится модель
в правой части уравнения содержится модель 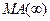 .
.
То есть 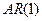 можно привести к
можно привести к 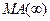 .
.
Выполним аналогичные преобразования для модели 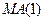 :
:
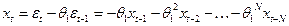 .
.
Таким образом, модель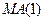 можно привести к
можно привести к 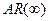 . При этом модель
. При этом модель 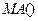 обладает свойством обратимости, если соответствующая ей модель
обладает свойством обратимости, если соответствующая ей модель 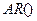 стационарна.
стационарна.
Смешанные модели 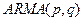 .
.
Смешанные модели авторегрессии и скользящего среднего имеют следующий вид: 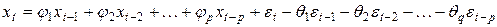 . (32)
. (32)
При помощи лагового оператора модель (32) записывается так:
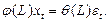 (33)
(33)
Модель стационарна, если стационарна входящая в нее модель авторегрессии, то есть корни уравнения 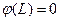 лежат вне единичного круга.
лежат вне единичного круга.
Для идентификации параметров модели 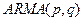 используют следующую таблицу, показывающую зависимость параметров модели от вида автокорреляционной и частной автокорреляционной функции:
используют следующую таблицу, показывающую зависимость параметров модели от вида автокорреляционной и частной автокорреляционной функции:
| Модель | ACF | PACF |
| Белый шум, MA(0) | 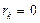 для k ≠ 0 для k ≠ 0 | 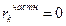 для k ≠ 0 для k ≠ 0 |
AR(1), 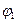 > 0 > 0 | Экспоненциальное убывание 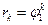 | 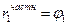 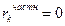 , k ≥ 2 , k ≥ 2 |
AR(1), 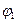 < 0 < 0 | Осциллирующее убывание 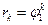 | 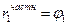 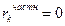 , k ≥ 2 , k ≥ 2 |
| AR(p) | Убывание к нулю с возможной осцилляцией | Нулевые значения при k ≥ p |
MA(1), 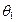 > 0 > 0 | Положительный пик при k = 1; зануление при k > 1 | Осциллирующее убывание; 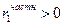 |
MA(1), 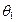 < 0 < 0 | Отрицательный пик при k = 1;зануление при k > 1 | Убывание по абсолютной величине; 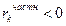 при k ≥ 1 при k ≥ 1 |
| MA(q) | Нулевые значения при k ≥ q | Убывание к нулю |
ARMA(1, 1), 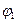 > 0 > 0 | Экспоненциальное убывание с лага 1; знак 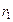 совпадает со знаком ( совпадает со знаком (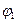 + +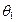 ) ) | Осциллирующее убывание с лага 1; 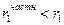 |
ARMA(1, 1), 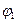 <0 <0 | Осциллирующее убывание с лага 1; знак 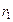 совпадает со знаком ( совпадает со знаком (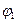 + +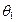 ) ) | Экспоненциальное убывание с лага 1; 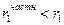 , знак , знак 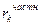 совпадает со знаком совпадает со знаком 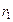 , k > 1 , k > 1 |
| ARMA(p, q) | Осциллирующее или прямое убывание, начинающееся с лага q | Осциллирующее или прямое убывание, начинающееся с лага p |
Модель 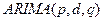 (модель Бокса и Дженкинса).
(модель Бокса и Дженкинса).
Рассмотренные выше модели 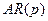 ,
, 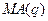 ,
, 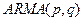 подходят для исследования стационарных временных рядов. Если временной ряд не стационарен, то применяются модели
подходят для исследования стационарных временных рядов. Если временной ряд не стационарен, то применяются модели 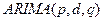 .
.
Введем в рассмотрение разностный оператор: 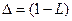 , тогда
, тогда 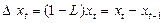 - результат применения разностного оператора. Результат применния разностного оператора порядка
- результат применения разностного оператора. Результат применния разностного оператора порядка 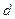 выглядит следующим образом:
выглядит следующим образом:
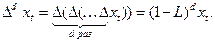 (34)
(34)
Если 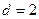 , то
, то 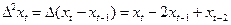 .
.
Вычисление разностей производится для приведения исходного ряда к стационарному ряду.
При наличии 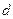 единичных корней характеристического уравнения
единичных корней характеристического уравнения 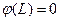 , разность порядка
, разность порядка 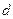 временного ряда
временного ряда 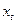 может быть представлена, как стационарный обратимый процесс следующего вида:
может быть представлена, как стационарный обратимый процесс следующего вида:
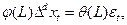 (35)
(35)
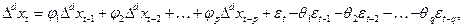 (36)
(36)
то есть разность порядка 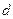 моделируется при помощи
моделируется при помощи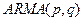 , оператор
, оператор 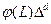 называется обобщенным оператором авторегрессии.
называется обобщенным оператором авторегрессии.
После замены 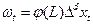 модель (36) примет следующий вид:
модель (36) примет следующий вид:
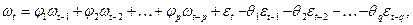 (37)
(37)
Далее делаем оценку параметров как в модели 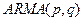 .
.
При возврате к исходным переменным выполняется следующее:
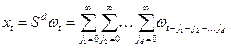 . (38)
. (38)
Для разности первого порядка:
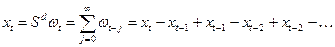 .
.
На основании модели 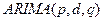 можно строить более общую модель, учитывающую авторегрессию и тренд сезонности. Такие модели имеют обозначение
можно строить более общую модель, учитывающую авторегрессию и тренд сезонности. Такие модели имеют обозначение 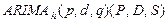 , где
, где 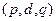 - параметры основного ряда,
- параметры основного ряда, 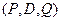 - параметры сезонного ряда, с числом
- параметры сезонного ряда, с числом 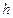 сезонов цикле.
сезонов цикле.
Пример построения модели 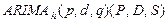 .
.
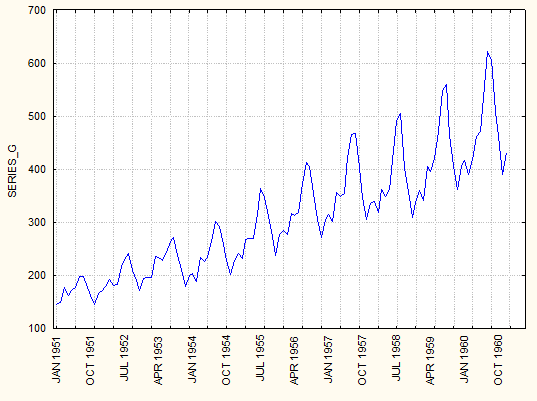
Поскольку ряд не стационарный, поэтому берем разность первого порядка. Преобразованный ряд и его автокорреляция выглядят следующим образом:
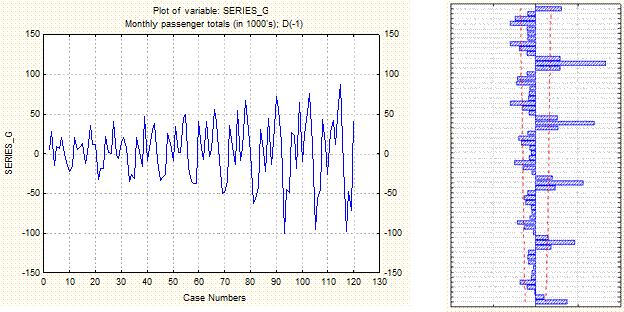
Ряд, который образует сезонность, также является не стационарным, поскольку коррелограмма показывает медленное убывание автокорреляции с периодом 12. Поэтому берем еще одну разность порядка 12 (порядок сезонности). Преобразованный ряд и его автокорреляция выглядят следующим образом:
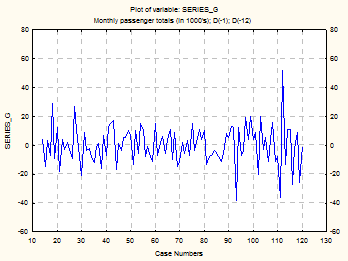
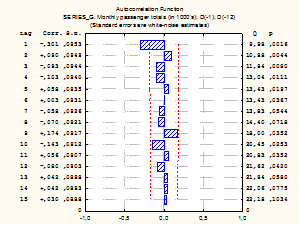
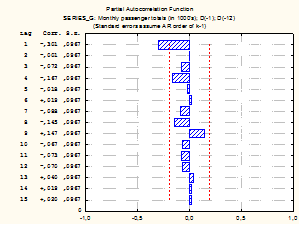
Наличие ненулевого значения автокорреляции на первом лаге свидетельствует о возможности использования для моделирования данного ряда моделей AR(1), MA(1) или ARMA(1,1). Моделью с наименьшей ошибкой оказалась модель MA(1).
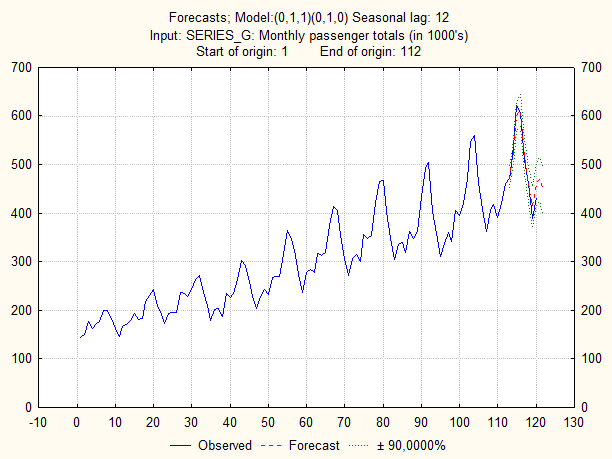
Таким образом, итоговой моделью ряда является 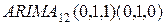 . Исходный ряд и прогнозные значения для последнего года представлены на следующем графике:
. Исходный ряд и прогнозные значения для последнего года представлены на следующем графике:
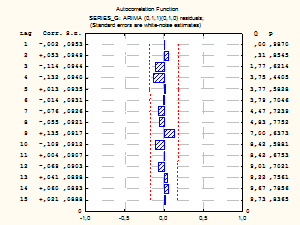
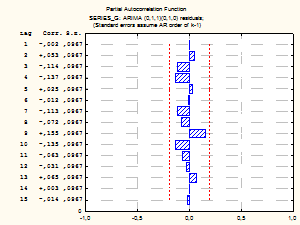
Автокорреляция и частная автокорреляция остатков модели.
 2014-01-25
2014-01-25 1430
1430