Условные математические ожидания

Условные математические ожидания и условные вероятности

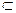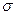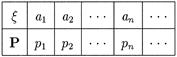
Пусть {W, F, Р } — вероятностное пространство и x = x (w) - заданная на нем случайная величина. Предположим, что A F - -алгебра и f(x) функция. Введем обозначение 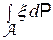, которое понимается так: а) если x - дискретная случайная величина с таблицей распределения

то 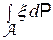= 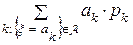, если же x - непрерывная случайная величина с плотностью распределения p(t), то 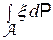= 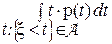. Аналогично можно определить и 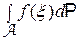(см. 2.3).

Определение 1. Условным математическим ожиданием случайной величины x относительно 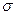-алгебры A называется случайная величина, обозначаемая 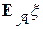или 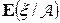, обладающая свойствами

1) она является A - измеримой;

2) для любого множества D из A выполняется = .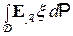

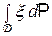Определение 2. Условной вероятностью случайного события B относительно 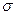-алгебры A называется случайная величина, обозначаемая 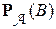и определяемая как 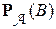= 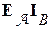, где 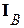= 1, если событие B произошло и 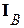= 0, если событие B не произошло.

Замечание. Из определения 1 следует, что для любого события С из A 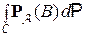= = 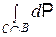P (С ∩ B).

Без доказательства перечислим некоторые свойства условного математического ожидания.

1. Если x постоянная, т.е. x = С с вероятностью 1, то 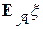= С с вероятностью 1.

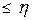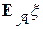
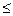
2. Если x с вероятностью 1, то 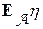с вероятностью 1.

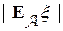
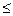
Следствие. Верно неравенство 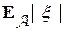с вероятностью 1.

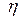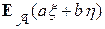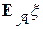3. Пусть x и случайные величины, a и b действительные числа, тогда = a+ b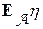c вероятностью 1.

4. Если 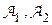две 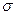-алгебры, такие, ч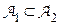то , то ==.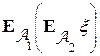

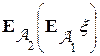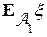5. Если x является A - измеримой, то 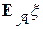= x.

6. Если A = { Ø, Ώ }, то = .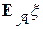

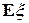7. Если x и A – независимы (т.е. x и 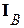независимы для любого события B из A), то = .

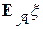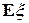8. Пусть x и 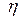случайные величины, 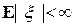и 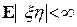, тогда = .

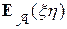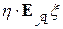Пусть h = h (w) – случайная величина, принимающая значения y ₁, y _2, …, y_n c положительными вероятностями. Обозначим через A(h) - 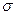- алгебру, состоящую из событий 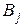, представимых в виде 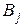= 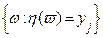; другими словами A(h) = 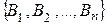. Тогда, согласно определениям 1 и 2, заменив A на A(h), величину 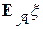мы назовем условным математическим ожиданием случайной величины x относительно случайной величины 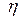, а величину 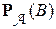назовем условной вероятностью события B относительно случайной величины .

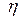Предположим теперь, что h ₁, h _2, …, h_n произвольные случайные величины. Обозначим через A(h ₁, h _2, …, h_n) = A(h) - 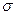- алгебру, состоящую из событий B, представимых в виде B = 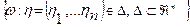. В этом случае также говорят, что A(h ₁, h _2, …, h_n) - 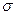-алгебра, порожденная случайными величинами h ₁, h _2, …, h_n. Также, согласно определениям 1 и 2, величину 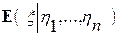= 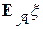мы назовем условным математическим ожиданием случайной величины x относительно случайных величин h ₁, h _2, …, h_n, а величину 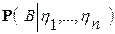= 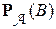назовем условной вероятностью события B относительно случайных величин h ₁, h _2, …, h_n, где A = A(h).

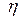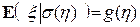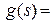
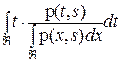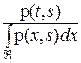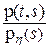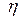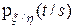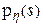Замечание. Пусть x и случайные величины, имеющие совместную плотность распределения p(t,s). Тогда , где . Здесь = называется плотностью условного распределения x относительно случайной величины , и обозначается как , где - плотность распределения случайной величины .

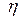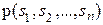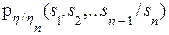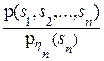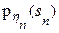Также, если предположить, что h ₁, h _2, …, h_n произвольные случайные величины, имеющие совместную плотность распределения , то мы можем определить плотность условного распределения, например, случайной величины h = (h _2, …, h_{n- 1}) относительно случайной величины h_n как = , где - плотность распределения случайной величины h_n.