Сглаживание временного ряда.
Идея данного метода заключается в замене элемента ряда на некоторое среднее значение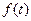 :
:
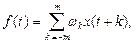 (16)
(16)
где 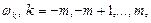 - некоторые весовые коэффициенты, такие что
- некоторые весовые коэффициенты, такие что 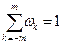 ,
,
величина 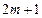 - окно сглаживания.
- окно сглаживания.
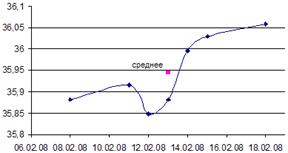
Следующий график демонстрирует 7 значений временного ряда (стоимость 1 евро) и рассчитанное относительно 4го значения «скользящее среднее» с окном 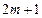 =7.
=7.
Поскольку, изменяя t от 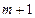 до
до 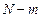 , при переходе от элемента ряда
, при переходе от элемента ряда 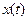 к
к 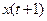 в правой части формулы (16) происходит замена лишь одного слагаемого
в правой части формулы (16) происходит замена лишь одного слагаемого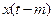 на
на 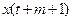 , то происходит «скольжение» по оси времени. Методы, основанные на формуле (16), называются методами скользящего среднего.
, то происходит «скольжение» по оси времени. Методы, основанные на формуле (16), называются методами скользящего среднего.
Определение коэффициентов 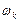 основано на следующей процедуре. В соответствии с теоремой Вейерштрасса любая гладкая функция
основано на следующей процедуре. В соответствии с теоремой Вейерштрасса любая гладкая функция 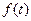 при самых общих допущениях (в ограниченном интервале изменения параметра
при самых общих допущениях (в ограниченном интервале изменения параметра 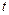 ) может быть представлена алгебраическим полиномом степени
) может быть представлена алгебраическим полиномом степени 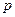 :
:

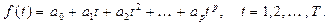 (17)
(17)
Поэтому для определения параметров 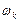 необходимо перебрать все окна сглаживания для
необходимо перебрать все окна сглаживания для
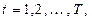 и при помощи метода наименьших квадратов подобрать параметры для полинома (17).
и при помощи метода наименьших квадратов подобрать параметры для полинома (17).
Однако, при проведении этой процедуры выясняется, что при решении задачи минимизации квадрата отклонения значения полинома 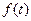 от значения ряда
от значения ряда 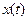 , на значения
, на значения 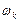 влияют лишь значения коэффициента
влияют лишь значения коэффициента 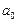 , независимо от порядка полинома.
, независимо от порядка полинома.
При использовании линейной функции формула (16) примет следующий вид:
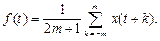 (18)
(18)
При использовании квадратичной функции формула (16) примет следующий вид:
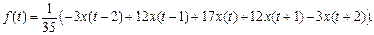 (19)
(19)
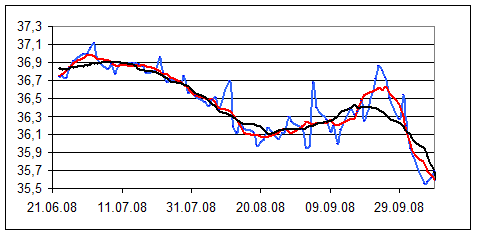
Следующий график отображает исходный временной ряд и скользящие средние с 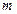 =7 и
=7 и 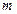 =17, параметр
=17, параметр  = 1 (линейная функция).
= 1 (линейная функция).
Для метода скользящих средних имеются таблицы со стандартными коэффициентами для разных значений  и
и  .
.
Экспоненциальное сглаживание (метод Брауна).
Идея метода заключается в том, чтобы при экстраполяции в будущее (прогноза) «недавним» значениям ряда придавать больший вес, чем более ранним значениям. Эту идею демонстрирует следующая формула:
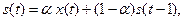 (20)
(20)
где 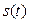 - сглаженный тренд в точке
- сглаженный тренд в точке 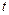 ,
, 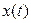 - значение временного ряда,
- значение временного ряда, 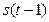 - сглаженное значение в точке
- сглаженное значение в точке 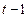 ,
, 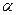 - коэффициент сглаживания.
- коэффициент сглаживания.
Покажем, что значение 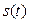 рекурсивно зависит от всех членов временного ряда:
рекурсивно зависит от всех членов временного ряда:
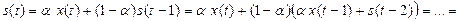
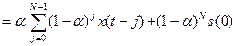 .
.
При 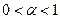 выполняется следующее:
выполняется следующее: 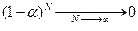 , поэтому последним слагаемым можно пренебречь. Таким образом, величина
, поэтому последним слагаемым можно пренебречь. Таким образом, величина 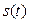 оказывается взвешенной суммой всех уровней ряда, причем веса уменьшаются экспоненциально, по мере углубления в историю процесса, отсюда название — экспоненциальная средняя.
оказывается взвешенной суммой всех уровней ряда, причем веса уменьшаются экспоненциально, по мере углубления в историю процесса, отсюда название — экспоненциальная средняя.
Экспоненциальное среднее имеет среднее значение, равное среднему исходного ряда, но
меньшую дисперсию.
Если 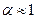 , то расхождение между сглаженным рядом и исходным рядом мало.
, то расхождение между сглаженным рядом и исходным рядом мало.
Если 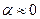 , то в большей степени подавляются колебания ряда и отчетливо вырисовывается тенденция.
, то в большей степени подавляются колебания ряда и отчетливо вырисовывается тенденция.
Сглаживание по формуле (20) подходит для сглаживания временных рядов с незначительным сезонным эффектом.
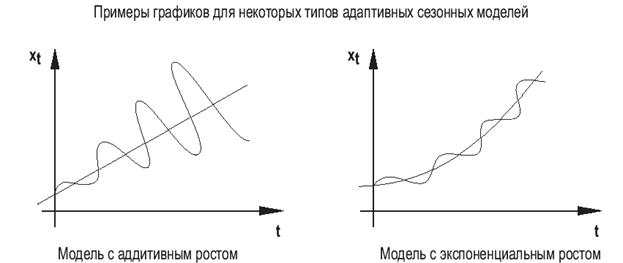
Для того, чтобы учесть наличие тренда и сезонности в исходном временном ряду применяются модели экспоненциального сглаживания следующего вида:
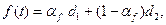 (21)
(21)
где 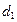 - величина, описывающая сезонность,
- величина, описывающая сезонность, 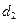 - величина, описывающая тренд.
- величина, описывающая тренд.
Величина, описывающая сезонность определяется следующим образом:
- если сезонности нет, то
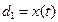 ,
, - при наличии аддитивной сезонности
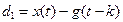 ,
, - при наличии мультипликативной сезонности
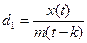 .
.
Таким образом, 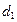 представляет собой текущую оценку процесса
представляет собой текущую оценку процесса 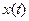 , очищенную от сезонных колебаний с помощью коэффициентов сезонности
, очищенную от сезонных колебаний с помощью коэффициентов сезонности 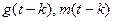 рассчитанных для предшествующего цикла.
рассчитанных для предшествующего цикла.
Величина, описывающая тренд определяется следующим образом:
- при отсутствии тренда
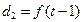 ,
, - при аддитивном росте значений ряда
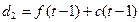 ,
, - мультипликативном росте
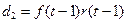 ,
,
Здесь 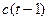 - абсолютный прирост, характеризующий изменение среднего уровня процесса, или аддитивный коэффициент роста,
- абсолютный прирост, характеризующий изменение среднего уровня процесса, или аддитивный коэффициент роста, 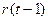 - коэффициент экспоненциального роста.
- коэффициент экспоненциального роста.
Адаптация всех перечисленных параметров осуществляется с помощью экспоненциального сглаживания:
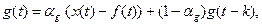
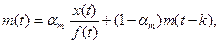
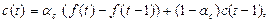
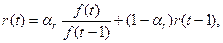
где 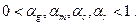
Задача оптимизации модели сводится к поиску наилучших значений параметров 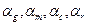 , выбор которых определяется целями исследования и характером моделируемого процесса.
, выбор которых определяется целями исследования и характером моделируемого процесса.
На следующем графике представлен исходный временной ряд и сглаживающая кривая, построенная с учетом аддитивной сезонности:
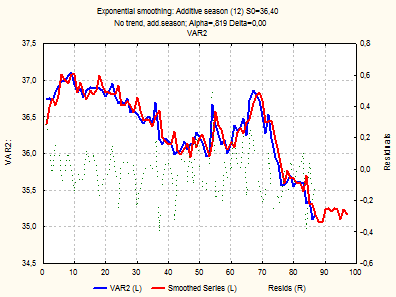
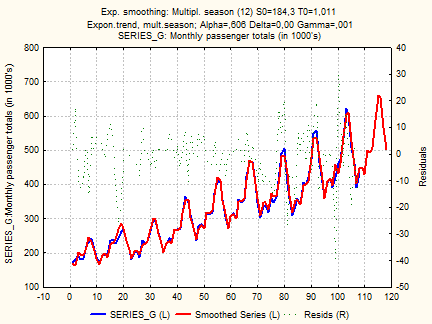
Для первого примера (перевозки пассажиров) сглаживание ряда и прогноз представлены на следующей диаграмме:
 2014-01-25
2014-01-25 760
760








