Интегральный признак Маклорена-Коши

Теорема 13. Пусть дан ряд с положительными членами (15) и существует функция 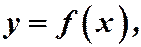такая, что

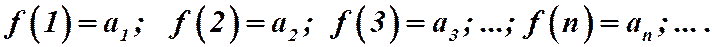
При этом функция 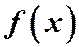непрерывна в промежутке 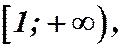положительна, и убывает в этом промежутке. Тогда, если интеграл 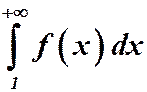сходится, то и ряд (1) сходится, а если интеграл 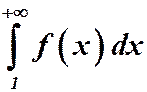расходится, то и ряд (15) расходится.

Пример 13. Исследовать на сходимость обобщенный гармонический ряд: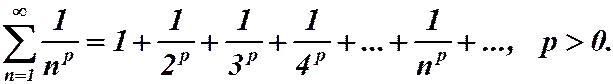

Решение. При 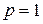имеем ряд: 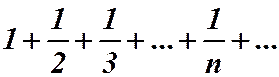. Это гармонический ряд, и он расходится.

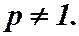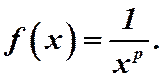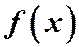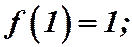
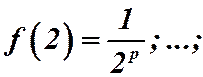
Пусть Рассмотрим функцию: Нетрудно проверить, что удовлетворяет всем условиям теоремы: 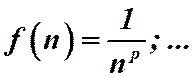. Эта функция непрерывна в промежутке 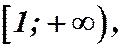положительна, и строго убывает.

Рассмотрим интеграл: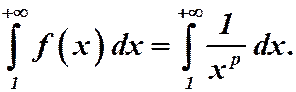

Из интегрального исчисления известно, что этот интеграл сходится при 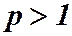и расходится при 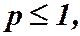значит, утверждаем, что обобщенный гармонический ряд сходится при 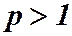и расходится при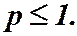

Пример14.

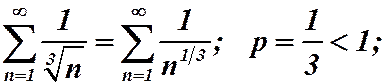ряд расходится.

Пример 15. 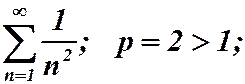ряд сходится.