Числовые ряды с положительными членами

Определение 3. Числовой ряд 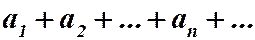называется рядом с положительными членами, если 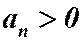при любом п.

Теорема 8. Любой ряд с положительными членами либо сходится, и его сумма есть положительное число, либо расходится и его сумма равна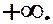

Доказательство. Пусть дан ряд с положительными членами:

.

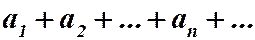Запишем последовательность частичных сумм:

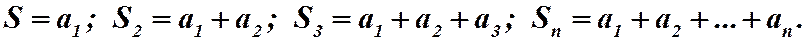
Очевидно, что .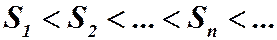

Таким образом, последовательность частичных сумм является строго возрастающей, но тогда возможны два случая:

1) Последовательность частичных сумм 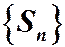ограничена сверху. По теореме Вейерштрасса о пределе монотонной ограниченной последовательности утверждаем, что 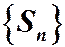имеет конечный предел, то есть ряд сходится.

2) Последовательность частичных сумм 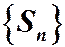возрастает неограниченно, тогда 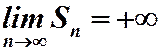, ряд расходится. Теорема доказана.