Групповая скорость определяется выражением:
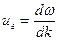 (32)
(32)
Определим отдельно выражения для 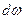 и
и 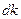 :
:
1) 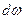 -?
-?
Из выражения 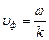 выразим угловую скорость:
выразим угловую скорость: 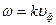 (33)
(33)
Продифференцируем это выражение по k: 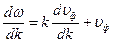 (34)
(34)
2) 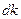 -?
-?
Выражения 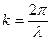 продифференцируем по
продифференцируем по 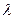 :
:
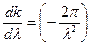
или 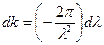 (35)
(35)
Подставим выражения (34) и (35) в выражение для групповой скорости (32), получим:
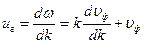 (36)
(36)
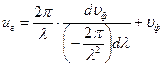 (37)
(37)
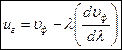 (38)
(38)
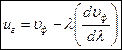 | - связь фазовой и групповой скорости |
Из (38) следует, что 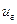 может быть как больше, так и меньше фазовой в зависимости от знака
может быть как больше, так и меньше фазовой в зависимости от знака 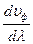 .
.
Если в среде не наблюдается дисперсия волн, то 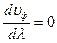 , тогда фазовая и групповая скорости совпадают
, тогда фазовая и групповая скорости совпадают 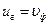 .
.
Понятие групповой скорости очень значимо, т.к. именно она фигурирует при измерении дальности радиолокации, в управлении космическими объектами.
Но 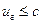 , а для
, а для 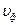 ограничений нет.
ограничений нет.
9. Нахождение групповой скорости методом Эренфеста
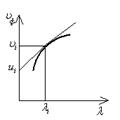 Зависимость групповой скорости от длины волны
Зависимость групповой скорости от длины волны 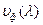 позволяет определить значение групповой скорости.
позволяет определить значение групповой скорости.
Для этого нужно провести касательную к точке с координатами 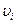 и
и 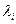 . Можно найти отрезок, отсекаемый касательной на оси ординат, равный значению групповой скорости.
. Можно найти отрезок, отсекаемый касательной на оси ординат, равный значению групповой скорости.
 2014-01-25
2014-01-25 1090
1090
