Если считать частицу свободной и движущейся по оси x, то U (x) = 0, уравнение Шредингера (2.14) примет вид
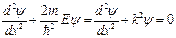 , (2.18)
, (2.18)
где k = 2 π / λ – волновой вектор электрона;
E = p 2/2 m = ћ 2 k 2 /2 m – его энергия.
Решением уравнения (2.18) будет функция
ψ = ψ 1 + ψ 2 = A exp(ikx) + B exp(- ikx), (2.19)
где А и В – постоянные коэффициенты.
С учетом (2.17) общее решение уравнения Шредингера будет иметь вид
Ψ(x, t) = A exp[ i (kx - ωt)] + B exp[- i (kx + ωt)]. (2.20)
Последнее уравнение выражает суперпозицию двух плоских волн, распространяющихся в противоположных направлениях. Для частицы, движущейся по оси x, B =0. Для частицы, движущейся в противоположном направлении, A =0.
Для трехмерного случая решением уравнения Шредингера будет являться выражение
Ψ = 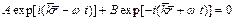 , (2.21)
, (2.21)
где 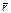 – радиус-вектор точки фронта волны.
– радиус-вектор точки фронта волны.
Энергия свободной частицы будет равняться
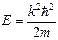 , (2.22)
, (2.22)
для трехмерного случая
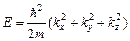 , (2.23)
, (2.23)
где kx, ky, kz – проекции волнового вектора на оси координат.
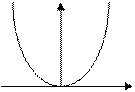
Выражения (2.22) и (2.23) показывают, что функция E (k) является непрерывной, т.е. энергетический спектр свободного электрона сплошной (рис. 2.1, а).
Поскольку микрочастица связана с плоской волной, имеет смысл рассмотреть вопрос о ее фазовой и групповой скоростях (п. 1.3).
В уравнении плоской волны, распространяющейся вдоль оси x, величина φ представляет собой фазу волны.
φ = k ∙ x - ω ∙ t, (2.24)
Напомним, что фазовая скорость υф – это скорость участка волны с постоянной фазой. Дифференцируя (2.24) с учетом постоянства фазы получим
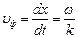 . (2.25)
. (2.25)
Подставляя в (2.25) значения ω и k, можно записать
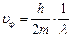 . (2.26)
. (2.26)
Анализ последнего выражения показывает, что фазовая скорость волн де Бройля зависит от их длины, т.е. имеет место эффект дисперсии.
Как отмечалось выше, в реальном случае частица представляет собой не монохроматическую волну, а волновой пакет, образованный двумя или более волнами, имеющими близкие значения длин и волновых векторов. Скорость этого пакета, групповая скорость Jгр
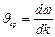 . (2.27)
. (2.27)
Подставив в последнее выражение значение k = mJ / ћ и производной d ω /d k = ħk / m, получим:
Jгр = J.
Последнее выражение показывает, что групповая скорость волн де Бройля равна скорости движения частицы.
В заключение рассмотрим вероятность нахождения свободного электрона в пространстве. Подставим в (2.8) выражение для плоской волны и получим w =const (рис. 2.1, б).
Это означает, что вероятность нахождения свободного электрона не зависит от координаты.

 E
E 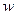
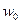
0 k 0 х
a) б)
Рис. 2.1. Свободный электрон: а – энергетический спектр; б – вероятность нахождения
 2015-02-04
2015-02-04 1499
1499
