Профили зубьев зубчатых колес выполнены по эвольвенте. Эвольвента (кривая BC на рис. 10.4) - это кривая, описываемая точкой отрезка, перекатываемого без скольжения по окружности; эту окружность называют основной. Эвольвентный профиль обеспечивает постоянство передаточного отношения передачи, 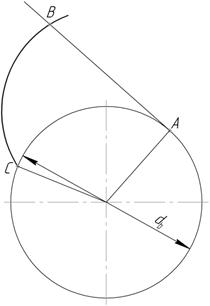 высокую прочность и долговечность зубьев колес, относительно малое скольжение на рабочих поверхностях зубьев и, следовательно, высокий КПД. Благодаря этим свойствам колеса с зубьями эвольвентного профиля получили широкое применение в машиностроении.
высокую прочность и долговечность зубьев колес, относительно малое скольжение на рабочих поверхностях зубьев и, следовательно, высокий КПД. Благодаря этим свойствам колеса с зубьями эвольвентного профиля получили широкое применение в машиностроении.
 Геометрия и основные параметры зубчатого зацепления цилиндрических прямозубых колес (нарезанных без смещения режущего инструмента) показаны на рис. 10.5:
Геометрия и основные параметры зубчатого зацепления цилиндрических прямозубых колес (нарезанных без смещения режущего инструмента) показаны на рис. 10.5:
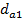 и
и 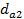 - диаметры окружностей выступов зубьев;
- диаметры окружностей выступов зубьев;
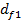 и
и 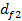 - диаметры окружностей впадин зубьев;
- диаметры окружностей впадин зубьев;
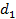 и
и 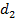 - диаметры делительных окружностей шестерни и колеса (на делительном диаметре толщина зуба равна ширине впадины, а их сумма - окружному делительному шагу);
- диаметры делительных окружностей шестерни и колеса (на делительном диаметре толщина зуба равна ширине впадины, а их сумма - окружному делительному шагу);
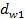 и
и 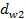 - диаметры начальных окружностей шестерни и колеса (начальные окружности перекатываются одна по другой без скольжения). Для зубчатых колес, нарезанных без смещения,
- диаметры начальных окружностей шестерни и колеса (начальные окружности перекатываются одна по другой без скольжения). Для зубчатых колес, нарезанных без смещения, 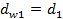 и
и 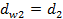 ;
;
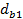 и
и 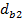 - диаметры основных окружностей шестерни и колеса;
- диаметры основных окружностей шестерни и колеса;
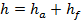 - высота зуба, где
- высота зуба, где 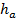 - высота головки зуба;
- высота головки зуба; 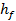 - высота ножки зуба (причем, обычно
- высота ножки зуба (причем, обычно 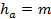 ,
, 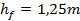 );
);
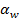 - угол зацепления стандартизован и равен
- угол зацепления стандартизован и равен 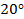 (угол между линией зацепления и прямой, перпендикулярной межосевой линии);
(угол между линией зацепления и прямой, перпендикулярной межосевой линии);
 - активная линия зацепления (траектория общей точки контакта сопряженных зубьев при ее движении);
- активная линия зацепления (траектория общей точки контакта сопряженных зубьев при ее движении);
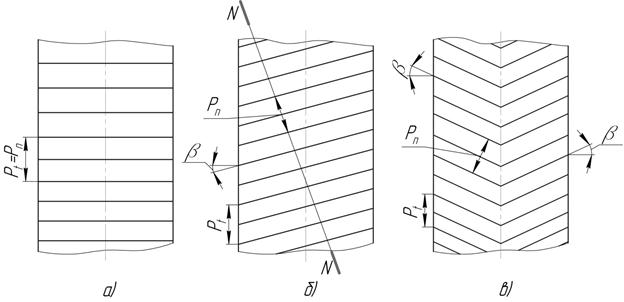
Рис. 10.6.
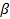 - угол наклона зубьев (угол между плоскостью, проходящей через ось зубчатого колеса и боковой поверхностью зуба), см. рис. 10.6, б и в. Угол наклона:
- угол наклона зубьев (угол между плоскостью, проходящей через ось зубчатого колеса и боковой поверхностью зуба), см. рис. 10.6, б и в. Угол наклона:
- для косых зубьев 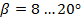 ;
;
- для шевронных зубьев 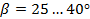 .
.
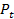 - окружной шаг зубьев (расстояние между одноименными профилями (точками) соседних зубьев по дуге концентрической окружности (делительной, начальной и т.д.) зубчатого колеса), см. рис. 10.6, а, б, в;
- окружной шаг зубьев (расстояние между одноименными профилями (точками) соседних зубьев по дуге концентрической окружности (делительной, начальной и т.д.) зубчатого колеса), см. рис. 10.6, а, б, в;
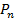 - нормальный шаг зубьев (косых, шевронных и арочных); кратчайшее расстояние (по нормали
- нормальный шаг зубьев (косых, шевронных и арочных); кратчайшее расстояние (по нормали 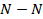 к профилю зуба) по одной из соосных поверхностей (делительной, начальной и т.д.) зубчатого колеса, см. рис. 10.6, б и в:
к профилю зуба) по одной из соосных поверхностей (делительной, начальной и т.д.) зубчатого колеса, см. рис. 10.6, б и в:
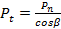 .
.
У прямозубых колес 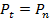 (рис. 10.6, а).
(рис. 10.6, а).
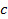 - радиальный зазор между головкой и впадиной зубьев сопряженного колеса;
- радиальный зазор между головкой и впадиной зубьев сопряженного колеса;
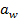 - межосевое расстояние, мм:
- межосевое расстояние, мм:
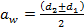 .
.
Знак минус подставляют для внутреннего зацепления.
При работе передачи в зацеплении находится одновременно одна или несколько пар зубьев. Количественной оценкой многопарности зацепления является коэффициент торцевого перекрытия:
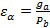 ,
,
где 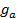 - длина активной линии зацепления (
- длина активной линии зацепления (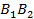 ). Например, если коэффициент торцевого перекрытия
). Например, если коэффициент торцевого перекрытия 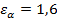 , то это значит, что
, то это значит, что 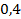 времени работы передачи в зацеплении находится одна пара зубьев, а
времени работы передачи в зацеплении находится одна пара зубьев, а 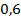 времени работы передачи - две пары зубьев.
времени работы передачи - две пары зубьев.
На практике для расчета 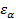 пользуются приближенной формулой:
пользуются приближенной формулой:
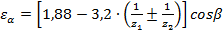 .
.
В прямозубых передачах коэффициент торцевого перекрытия 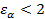 (обычно
(обычно 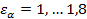 ), в косозубых, шевронных и с круговым зубом -
), в косозубых, шевронных и с круговым зубом - 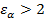 . С увеличением коэффициента перекрытия повышается плавность зацепления зубьев, уменьшаются динамические нагрузки на них и снижается шум, возникающий при работе передачи. Поэтому в быстроходных и высоконагруженных передачах вместо прямых зубьев применяют косые, шевронные и арочные зубья.
. С увеличением коэффициента перекрытия повышается плавность зацепления зубьев, уменьшаются динамические нагрузки на них и снижается шум, возникающий при работе передачи. Поэтому в быстроходных и высоконагруженных передачах вместо прямых зубьев применяют косые, шевронные и арочные зубья.
Для прямозубых колес длина окружности делительного диаметра 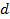 связана с числом зубьев
связана с числом зубьев 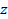 и шагом
и шагом 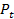 :
:
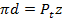 ⇒
⇒ 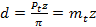 ,
,
где 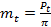 - окружной модуль зубьев. Тогда для косых, шевронных и арочных зубьев модуль определяется также в нормальном направлении и называется нормальным модулем:
- окружной модуль зубьев. Тогда для косых, шевронных и арочных зубьев модуль определяется также в нормальном направлении и называется нормальным модулем:
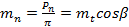 .
.
Для прямых зубьев 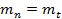 .
.
Так как делительная окружность является базовой при определении размеров зубьев, то размеры зубьев цилиндрических зубчатых колес вычисляют по делительному нормальному модулю, который называют модулем зацепления 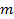 . Модуль зацепления
. Модуль зацепления 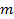 - основная характеристика размеров зубчатых и червячных колес. Модули стандартизованы в диапазоне
- основная характеристика размеров зубчатых и червячных колес. Модули стандартизованы в диапазоне 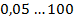 мм (ГОСТ 9563-60).
мм (ГОСТ 9563-60).
 2014-01-25
2014-01-25 973
973








