При построении планов ускорений точек кулисного механизма будем использовать обозначения соответствующих точек и разложение движения звеньев, принятые при построении планов скоростей.
Определяем ускорение точки B1, принадлежащей вращающемуся звену 1. Ускорение точки B1 является векторной суммой нормального и тангенциального ускорений:


 aB1 = aB1 + aB1.
aB1 = aB1 + aB1.
 B® O1 ^ O1B
B® O1 ^ O1B
Модуль нормального ускорения:
| aB1 | = ω1·lO1B [м/с²].
Вектор нормального ускорения всегда направлен к центру кривизны траектории точки. В нашем
 случае a B 1 направлен от В к O1 (B O1).
случае a B 1 направлен от В к O1 (B O1).
Модуль тангенциального ускорения:
| aB1 | = ε 1·lO1B [м/с²].
Вектор тангенциального ускорения направлен всегда по касательной к траектории точки (перпендикулярно мгновенному радиусу вращения) в сторону углового ускорения ε.
 Угловое ускорение первого звена ε1 = = 0, поскольку ω1 = const. Следовательно a B1 = 0. Отсюда:
Угловое ускорение первого звена ε1 = = 0, поскольку ω1 = const. Следовательно a B1 = 0. Отсюда:

 aB1 = aB1.
aB1 = aB1.
 Из произвольно выбранной точки Pa - полюса плана ускорений – проводим прямую, параллельную BO1 и в направлении от В к O1 откладываем отрезок Pab1, изображающий вектор абсолютного ускорения aB 1 (рис. 4).
Из произвольно выбранной точки Pa - полюса плана ускорений – проводим прямую, параллельную BO1 и в направлении от В к O1 откладываем отрезок Pab1, изображающий вектор абсолютного ускорения aB 1 (рис. 4).
                   Pa Pa
|| O2B
aB3 ||BO1
n3 aB1,2
aB3 aB3
┴ O2B b1,2
aB2
|| BO2 k
aB2 - B3
b3 aC5
|| x - x
aC3,4
aC4 – C5
c3,4 ^ x – x c5
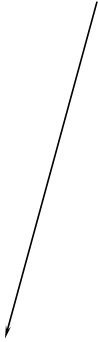
Рисунок 4 – План ускорений механизма
|
Определяем масштабный коэффициент линейных ускорений:
μa = [ ].
Дальнейшее построение плана ускорений механизма будем выполнять с учетом выбранного масштабного коэффициента μ a.
Определяем ускорение точки B2. Как и абсолютная линейная скорость точки B 2, ускорение точки B 2 равно по модулю и направлению ускорению точки B 1:

 aB2 = aB1.
aB2 = aB1.

 На плане ускорений aB2 изображается тем же отрезком, что и aB1 – P ab1,2.
На плане ускорений aB2 изображается тем же отрезком, что и aB1 – P ab1,2.
 Определяем ускорение точки B3. Для этого воспользуемся разложением сложного движения звена 2, как и при определении абсолютной линейной скорости VB3:
Определяем ускорение точки B3. Для этого воспользуемся разложением сложного движения звена 2, как и при определении абсолютной линейной скорости VB3:



 aB2 = aB2 + aB2 + aB2. [1]
aB2 = aB2 + aB2 + aB2. [1]
Абсолютное ускорение точки B2 в сложном движении является векторной суммой переносного, относительного и кориолисового ускорений.
Переносное движение – возвратно-вращательное движение кулисы 3. Следовательно переносное ускорение точки B 2 ползуна равно абсолютному ускорению точки B3 кулисы:

 aB2 = aB3.
aB2 = aB3.
Звено 3 совершает возвратно-вращательное движение, поэтому абсолютное ускорение точки B3 является векторной суммой нормального и тангенциального ускорений:
aB3 = aB3 + aB3.
 Вектор нормального ускорения aB3 направлен от В к O2. Модуль нормального ускорения:
Вектор нормального ускорения aB3 направлен от В к O2. Модуль нормального ускорения:
| aB3| = ω3·lO2B = [м/с²].



Вектор тангенциального ускорения
aB3 направлен перпендикулярно
O1B. Модуль
| aB3 | определить не можем, т.к. нам неизвестен закон изменения
ω3 = f(t ).
Относительное ускорение aB2 в относительном движении направлено вдоль кулисы:

 aB2 = aB2 – B3.
aB2 = aB2 – B3.
|| BO2
Кориолисово ускорение равно двойному векторному произведению угловой скорости переносного движения и линейной скорости относительного движения:


 aB2 = 2ω2 ´VB2.
aB2 = 2ω2 ´VB2.
Угловая скорость переносного движения ω2 в нашем случае равна угловой скорости звена 3:

 ω2 = ω3.
ω2 = ω3.
Относительная линейная скорость VB2 в нашем случае равна относительной скорости поступательного перемещения точки B2 по отношению к точке B3:
V B2 = V B2 - B3.

 Можно определить a B2 = 2ω3 ´ V B2 - B3.
Можно определить a B2 = 2ω3 ´ V B2 - B3.
Определяем модуль кориолисового ускорения:

 | aB2 | = 2|ω3|·|V B2 - B3|sin α,
| aB2 | = 2|ω3|·|V B2 - B3|sin α,

 где α – угол между направлениями векторов угловой ω3 и линейной V B2 - B3 скоростей.
где α – угол между направлениями векторов угловой ω3 и линейной V B2 - B3 скоростей.
 В нашем случае вектор угловой скорости ω 3 направлен перпендикулярно плоскости чертежа к нам
В нашем случае вектор угловой скорости ω 3 направлен перпендикулярно плоскости чертежа к нам
(по правилу буравчика). Вектор относительной скорости V B2 - B3 лежит в плоскости чертежа. Угол между векторами угловой и относительной скоростей α = 90°,sin α = sin 90° = 1, следовательно:
 | aB2 | = 2ω3· V B2 - B3.
| aB2 | = 2ω3· V B2 - B3.


Определяем направление вектора кориолисового ускорения по методу Н.Е.Жуковского. Для определения направления вектора кориолисового ускорения необходимо вектор относительной скорости (относительного движения) повернуть в направлении переносной угловой скорости на 90°. (Переносим
V B2 - B3 на план механизма и поворачиваем его на 90° по ходу
ω3). В нашем случае
aB2 ^ BO2.
Подставим в исходное уравнение [1] полученные данные:




 aB2 = aB3 + aB3 + aB2 – B3 + aB2.
aB2 = aB3 + aB3 + aB2 – B3 + aB2.




 B O2 ^ BO2 || BO2 ^ BO2
B O2 ^ BO2 || BO2 ^ BO2



Получаем векторное уравнение с двумя скалярными неизвестными: модулями ускорений
| aB3| и
| aB2 – B3|. Решаем уравнение графическим методом. Из полюса плана ускорений
Pa проводим линию параллельно
BO2 – направление нормального ускорения точки
B3 - aB3.
Определяем длину отрезка на плане ускорений:
Pan3 = [мм].

Откладываем отрезок
Pan3 и конец вектора обозначаем
n3. Через точку
n 3 на плане ускорений проводим линию
^ BO2 (а следовательно и
^ Pan3) – направление тангенциального ускорения
aB3.
Вектор aB2 является замыкающим в сумме векторов. Определим длину отрезка kb1,2 =, откладываем





отрезок на плане ускорений
^ BO2 и направляем вектор в точку
b1,2. Затем через точку
k проводим линию параллельно
BO2, направление вектора относительного ускорения
aB2–B3, до пересечения с направлением тангенциального ускорения
aB3. Полученную точку пересечения обозначаем
b3. Проставляем направление векторов
aB3 и
aB2 – B3 по правилу сложения векторов. Соединяем
Pa с точкой
b3 на плане ускорений. Отрезок
Pab3 является изображением вектора абсолютного ускорения точки
B3 -
aB3. Определяем модули ускорений:


 | aB3| = (Pab3) μa; | aB3| = (n3b3) μa; | aB2 – B3 | = (b3k) μa.
| aB3| = (Pab3) μa; | aB3| = (n3b3) μa; | aB2 – B3 | = (b3k) μa.
Определяем ускорение точки
C3, принадлежащей звену
3. Для этого воспользуемся теоремой о подобии. Составляем пропорцию:
aC3CO2 Pac3
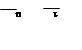


 aB1 = aB1 + aB1.
aB1 = aB1 + aB1. B® O1 ^ O1B
B® O1 ^ O1B
 случае a B 1 направлен от В к O1 (B O1).
случае a B 1 направлен от В к O1 (B O1).
 Угловое ускорение первого звена ε1 = = 0, поскольку ω1 = const. Следовательно a B1 = 0. Отсюда:
Угловое ускорение первого звена ε1 = = 0, поскольку ω1 = const. Следовательно a B1 = 0. Отсюда:
 aB1 = aB1.
aB1 = aB1. Из произвольно выбранной точки Pa - полюса плана ускорений – проводим прямую, параллельную BO1 и в направлении от В к O1 откладываем отрезок Pab1, изображающий вектор абсолютного ускорения aB 1 (рис. 4).
Из произвольно выбранной точки Pa - полюса плана ускорений – проводим прямую, параллельную BO1 и в направлении от В к O1 откладываем отрезок Pab1, изображающий вектор абсолютного ускорения aB 1 (рис. 4).

















 Pa
Pa

 aB2 = aB1.
aB2 = aB1.
 На плане ускорений aB2 изображается тем же отрезком, что и aB1 – P ab1,2.
На плане ускорений aB2 изображается тем же отрезком, что и aB1 – P ab1,2. Определяем ускорение точки B3. Для этого воспользуемся разложением сложного движения звена 2, как и при определении абсолютной линейной скорости VB3:
Определяем ускорение точки B3. Для этого воспользуемся разложением сложного движения звена 2, как и при определении абсолютной линейной скорости VB3:


 aB2 = aB2 + aB2 + aB2. [1]
aB2 = aB2 + aB2 + aB2. [1]
 aB2 = aB3.
aB2 = aB3.

 Вектор нормального ускорения aB3 направлен от В к O2. Модуль нормального ускорения:
Вектор нормального ускорения aB3 направлен от В к O2. Модуль нормального ускорения:


 Вектор тангенциального ускорения aB3 направлен перпендикулярно O1B. Модуль | aB3 | определить не можем, т.к. нам неизвестен закон изменения ω3 = f(t ).
Вектор тангенциального ускорения aB3 направлен перпендикулярно O1B. Модуль | aB3 | определить не можем, т.к. нам неизвестен закон изменения ω3 = f(t ).

 aB2 = aB2 – B3.
aB2 = aB2 – B3.

 aB2 = 2ω2 ´VB2.
aB2 = 2ω2 ´VB2.

 ω2 = ω3.
ω2 = ω3.



 Можно определить a B2 = 2ω3 ´ V B2 - B3.
Можно определить a B2 = 2ω3 ´ V B2 - B3.

 | aB2 | = 2|ω3|·|V B2 - B3|sin α,
| aB2 | = 2|ω3|·|V B2 - B3|sin α,
 где α – угол между направлениями векторов угловой ω3 и линейной V B2 - B3 скоростей.
где α – угол между направлениями векторов угловой ω3 и линейной V B2 - B3 скоростей. В нашем случае вектор угловой скорости ω 3 направлен перпендикулярно плоскости чертежа к нам
В нашем случае вектор угловой скорости ω 3 направлен перпендикулярно плоскости чертежа к нам


 | aB2 | = 2ω3· V B2 - B3.
| aB2 | = 2ω3· V B2 - B3.
 Определяем направление вектора кориолисового ускорения по методу Н.Е.Жуковского. Для определения направления вектора кориолисового ускорения необходимо вектор относительной скорости (относительного движения) повернуть в направлении переносной угловой скорости на 90°. (Переносим V B2 - B3 на план механизма и поворачиваем его на 90° по ходу ω3). В нашем случае aB2 ^ BO2.
Определяем направление вектора кориолисового ускорения по методу Н.Е.Жуковского. Для определения направления вектора кориолисового ускорения необходимо вектор относительной скорости (относительного движения) повернуть в направлении переносной угловой скорости на 90°. (Переносим V B2 - B3 на план механизма и поворачиваем его на 90° по ходу ω3). В нашем случае aB2 ^ BO2.






 aB2 = aB3 + aB3 + aB2 – B3 + aB2.
aB2 = aB3 + aB3 + aB2 – B3 + aB2.



 B O2 ^ BO2 || BO2 ^ BO2
B O2 ^ BO2 || BO2 ^ BO2

 Получаем векторное уравнение с двумя скалярными неизвестными: модулями ускорений | aB3| и | aB2 – B3|. Решаем уравнение графическим методом. Из полюса плана ускорений Pa проводим линию параллельно BO2 – направление нормального ускорения точки B3 - aB3.
Получаем векторное уравнение с двумя скалярными неизвестными: модулями ускорений | aB3| и | aB2 – B3|. Решаем уравнение графическим методом. Из полюса плана ускорений Pa проводим линию параллельно BO2 – направление нормального ускорения точки B3 - aB3.

 Откладываем отрезок Pan3 и конец вектора обозначаем n3. Через точку n 3 на плане ускорений проводим линию ^ BO2 (а следовательно и ^ Pan3) – направление тангенциального ускорения aB3.
Откладываем отрезок Pan3 и конец вектора обозначаем n3. Через точку n 3 на плане ускорений проводим линию ^ BO2 (а следовательно и ^ Pan3) – направление тангенциального ускорения aB3.





 отрезок на плане ускорений ^ BO2 и направляем вектор в точку b1,2. Затем через точку k проводим линию параллельно BO2, направление вектора относительного ускорения aB2–B3, до пересечения с направлением тангенциального ускорения aB3. Полученную точку пересечения обозначаем b3. Проставляем направление векторов aB3 и aB2 – B3 по правилу сложения векторов. Соединяем Pa с точкой b3 на плане ускорений. Отрезок Pab3 является изображением вектора абсолютного ускорения точки B3 - aB3. Определяем модули ускорений:
отрезок на плане ускорений ^ BO2 и направляем вектор в точку b1,2. Затем через точку k проводим линию параллельно BO2, направление вектора относительного ускорения aB2–B3, до пересечения с направлением тангенциального ускорения aB3. Полученную точку пересечения обозначаем b3. Проставляем направление векторов aB3 и aB2 – B3 по правилу сложения векторов. Соединяем Pa с точкой b3 на плане ускорений. Отрезок Pab3 является изображением вектора абсолютного ускорения точки B3 - aB3. Определяем модули ускорений:


 | aB3| = (Pab3) μa; | aB3| = (n3b3) μa; | aB2 – B3 | = (b3k) μa.
| aB3| = (Pab3) μa; | aB3| = (n3b3) μa; | aB2 – B3 | = (b3k) μa. 2014-01-25
2014-01-25 714
714








