Примечание
Примечание 2
Оператор 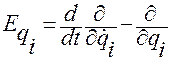 называется оператором Эйлера-Лагранжа.
называется оператором Эйлера-Лагранжа.
Через него формула Лагранжа записывается в следующей форме
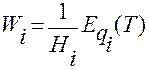 ,
,
где
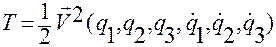 .
.
В конце этой лекции в Дополнениях 2.1 и 2.2 к главе 1 показывается расчет кинематических характеристик точки на примере цилиндрических координат (§6) и сферических координат (§7).
Дополнения к лекции 4 по главе 1 «Кинематика точки»
1. Дополнения к §5
§5. Задание движения материальной точки
в криволинейных координатах
1.1. Дополнение 1 к §5
7º. Союзная система координат и ее связь с основной. Ковариантные координаты вектора
Поясним смысл терминов «ковариантные» и «контравариантные» координаты, которые введены в §5 в пункте 7.
В указанном пункте доказали формулу (1.5.23):
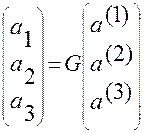 . (1.5.23)
. (1.5.23)
где
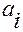 ,
, 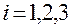 , — координаты вектора
, — координаты вектора 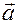 в союзной системе,
в союзной системе,
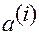 ,
, 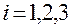 , — координаты этого же вектора в основной
, — координаты этого же вектора в основной
системе,
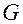 — матрица метрических коэффициентов
— матрица метрических коэффициентов
основной системы.
Из (1.5.23) заключаем, что 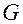 имеет второй смысл.
имеет второй смысл.
Она является матрицей перехода от основной системы к союзной системе координат.
Заметим, что основное правило, по которому осуществляется расчет координат вектора 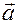 в любой новой системе координат по координатам этого вектора, известным в некоторой фиксированной аффинной системе, является соотношение вида
в любой новой системе координат по координатам этого вектора, известным в некоторой фиксированной аффинной системе, является соотношение вида
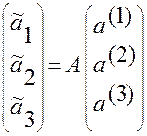 , (1.5.24)
, (1.5.24)
где
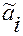 — координаты вектора
— координаты вектора 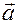 в «новой системе» координат,
в «новой системе» координат,
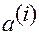 ,
, 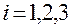 , — координаты вектора
, — координаты вектора 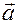 в заданной
в заданной
(фиксированной, «старой») системе,
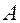 — неособая матрица, называемая матрицей перехода от
— неособая матрица, называемая матрицей перехода от
«старой» системы к «новой» системе координат.
Фиксируем неособую матрицу 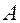 .
.
Будем говорить, что координаты 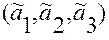 любого вектора
любого вектора 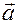 согласованно изменяются по отношению к его координатам
согласованно изменяются по отношению к его координатам 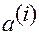 ,
, 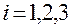 , заданным в фиксированной основной системе координат, если они рассчитываются по формуле (1.5.24).
, заданным в фиксированной основной системе координат, если они рассчитываются по формуле (1.5.24).
Система координат, для которой 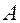 является матрицей перехода от фиксированной основной системы, называется согласованной с основной системой через матрицу
является матрицей перехода от фиксированной основной системы, называется согласованной с основной системой через матрицу 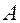 .
.
Из (1.5.23)
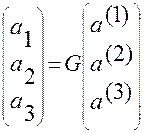 (1.5.23)
(1.5.23)
следует, что союзная система является согласованной с основной через матрицу 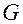 метрических коэффициентов основной системы.
метрических коэффициентов основной системы.
Поэтому координаты векторов 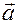 в этой (союзной) системе называются ковариантными (слово «ковариантные» в переводе с французского означает «согласованно изменяющиеся»).
в этой (союзной) системе называются ковариантными (слово «ковариантные» в переводе с французского означает «согласованно изменяющиеся»).
Они согласованно изменяются через матрицу 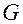 .
.
Основные координаты вектора 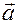 могут быть вычислены через согласованные координаты
могут быть вычислены через согласованные координаты 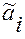 (координаты этого вектора в новой системе координат) при фиксированной матрице
(координаты этого вектора в новой системе координат) при фиксированной матрице 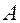 по формуле
по формуле
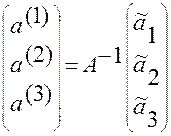 . (1.5.25)
. (1.5.25)
Очевидно, матрица 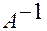 является матрицей перехода от «новой» системы координат к «старой» (основной) системе.
является матрицей перехода от «новой» системы координат к «старой» (основной) системе.
В этом случае выражение (1.5.25) можем трактовать как обратный закон пересчета координат, а координаты 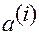 вектора
вектора 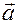 в основной («старой») системе могут рассматриваться как координаты «противоположно меняющиеся» при фиксированной матрице
в основной («старой») системе могут рассматриваться как координаты «противоположно меняющиеся» при фиксированной матрице 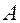 по отношению к новым координатам.
по отношению к новым координатам.
Поэтому координаты вектора 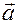 в основной системе (координаты
в основной системе (координаты 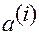 ) по отношению к союзной системе принято называть контравариантными координатами (при переводе с французского языка слово «контравариантные» означает «обратно изменяющиеся»).
) по отношению к союзной системе принято называть контравариантными координатами (при переводе с французского языка слово «контравариантные» означает «обратно изменяющиеся»).
Термин «контравариантные координаты» имеет и другой смысл.
А именно, он означает, что эти координаты меняются (рассчитываются) по обратному закону относительно некоторой фиксированной системы координат.
Если матрица 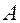 задана, то согласно определению 9 эти координаты согласованы с заданной фиксированной системой координат через обратную матрицу
задана, то согласно определению 9 эти координаты согласованы с заданной фиксированной системой координат через обратную матрицу 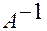 .
.
Применим это правило к основной и союзной системам координат.
Если считать, что координаты союзной системы фиксированы (заданы), а основной — пересчитываются по ним, то этот пересчет осуществляется с помощью обратной матрицы 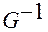 .
.
А тогда согласно указанному выше правилу:
координаты основной системы следует называть «контравариантными», поскольку они согласованы с фиксированными (союзными) через обратную матрицу 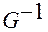 .
.
1.2. Дополнение 2 к §5
8º. Скорость точки в криволинейной системе координат. Лемма Лагранжа
 2014-01-25
2014-01-25 702
702








