Дополнение 2 к главе 1
§7. Кинематические характеристики точки
в сферических координатах.
Как показано в §5,формулы связи декартовых и сферических координат имеют вид:
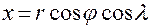 ,
,
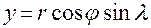 ,
,
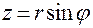 ,
,
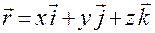 .
.
Полагаем
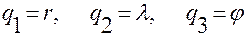 .
.
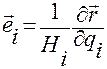 ,
, 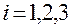 .
.
Коэффициенты Ламе 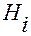 будут выражаться через криволинейные координаты
будут выражаться через криволинейные координаты 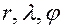 по формулам:
по формулам:
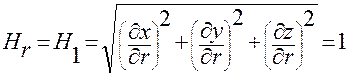 ;
;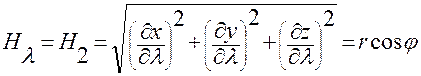 ;
;
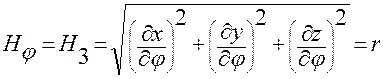 .
.
А тогда
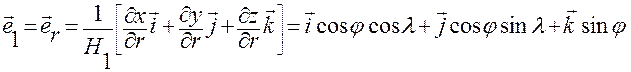 ,
,
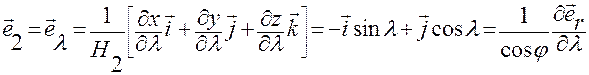 ,
,
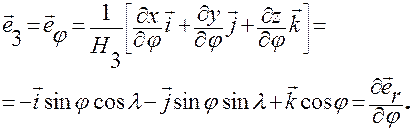
2. Легко показать, что
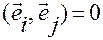 ,
, 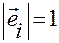 ,
, 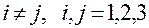 ,
,
т.е. сферическая система координат — ортогональная.
3. Вычислим скорость 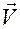 в проекциях на орты
в проекциях на орты 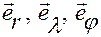 , т.е. вычислим ковариантные координаты
, т.е. вычислим ковариантные координаты 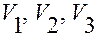 скорости
скорости 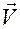 .
.
Поскольку сферическая система координат ортогональная, то
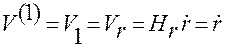 ,
,
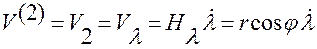 ,
,
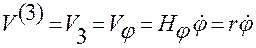 ,
,
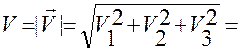
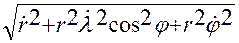 .
.
Из этих соотношений легко находятся направляющие косинусы 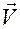 в системе
в системе 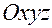 :
:
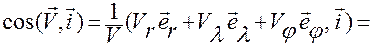
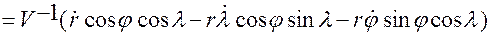 ,
,
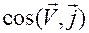
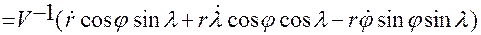 ,
,
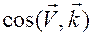
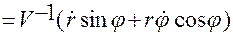 .
.
4. Вычислим ускорение 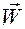 в проекциях на орты
в проекциях на орты 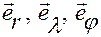 , используя формулу Лагранжа.
, используя формулу Лагранжа.
Для этого построим 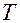 :
:
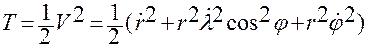 .
.
Тогда
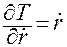 ,
, 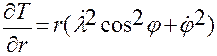 .
.
Отсюда, применяя формулу Лагранжа, находим
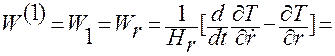
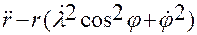 . (1.7.1)
. (1.7.1)
Аналогично для 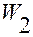 получаем
получаем
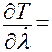
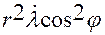 ,
, 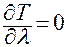 ,
,
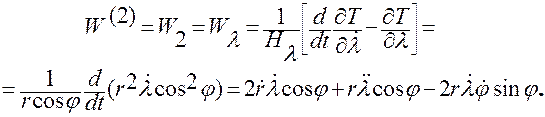 (1.7.2)
(1.7.2)
В свою очередь для 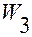 будем иметь
будем иметь
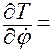
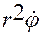 ,
, 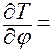
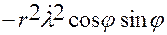 ,
,
 (1.7.3)
(1.7.3)
5. Подстановкой (1.7.1), (1.7.2), (1.7.3) в формулу 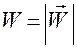
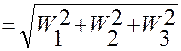 можем выписать выражение для модуля ускорения
можем выписать выражение для модуля ускорения 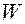 .
.
6. Подстановка 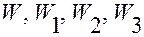 в соотношения
в соотношения
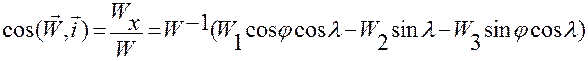 ,
,
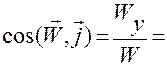
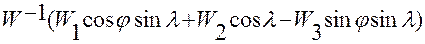 ,
,
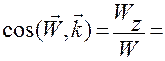
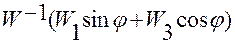
дает зависимости направляющих косинусов вектора 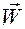 в системе
в системе 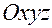 от криволинейных координат
от криволинейных координат 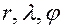 , обобщенных скоростей
, обобщенных скоростей 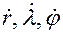 и обобщенных ускорений
и обобщенных ускорений 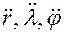 .
.
 2014-01-25
2014-01-25 713
713








