Ковариантные координаты ускорения точки
Построим формулу Лагранжа для вычисления ковариантных координат 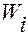 ,
, 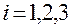 , ускорения
, ускорения 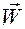 .
.
Согласно определению ковариантных координат можем записать
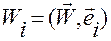 ,
, 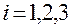 .
.
Подставим в правую часть этого равенства значение орта 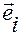 , вычисленное в точке
, вычисленное в точке 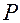 ,
,
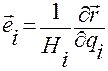 .
.
Вынесем 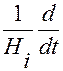 за знак скалярного произведения.
за знак скалярного произведения.
В результате придем к следующему выражению для 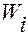 :
:
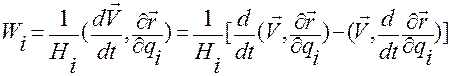 .
.
В нем, в соответствии с определением понятия ускорения точки, производная 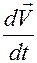 вычисляется вдоль движения
вычисляется вдоль движения
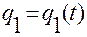 ,
, 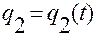 ,
, 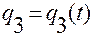 .
.
Поэтому в множителе 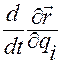 производная по времени строится от суперпозиции функций
производная по времени строится от суперпозиции функций 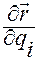 и
и 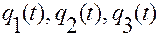 .
.
А потому, согласно свойству б) функции 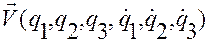 из леммы Лагранжа, множитель
из леммы Лагранжа, множитель 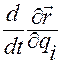 можно заменить производной
можно заменить производной 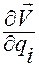 .
.
Кроме того, по свойству а) из той же леммы, множитель 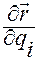 можно заменить производной
можно заменить производной 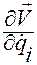 .
.
А тогда выражение для 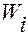 примет вид
примет вид
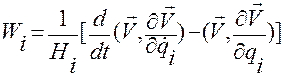 . (1.5.39)
. (1.5.39)
Введем функцию
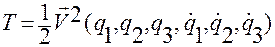 ,
,
где 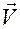 задается формулой (1.5.32):
задается формулой (1.5.32):
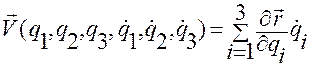
 . (1.5.32)
. (1.5.32)
Будем иметь
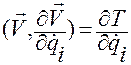 ,
, 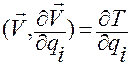 .
.
Подставляя в (1.5.39)
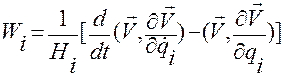 , (1.5.39)
, (1.5.39)
окончательно найдем
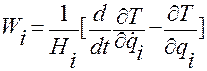 ,
, 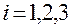 . (1.5.40)
. (1.5.40)
Эта формуланазывается формулой Лагранжа для вычисления ковариантных координат ускорения точки.
Таким образом, доказали следующую теорему.
Ковариантные координаты вектора 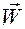 ускорения материальной точки выражаются по формуле(1.5.40).
ускорения материальной точки выражаются по формуле(1.5.40).
Если криволинейные координаты ортогональны, то 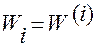 ,
, 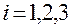 .
.
В таком случае формула (1.5.39) позволяет вычислить контравариантные координаты 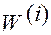 вектора
вектора 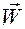 .
.
 2014-01-25
2014-01-25 709
709







