Бетонные спиральные камеры большей частью имеют тавровые поперечные сечения (рис. 7.5), так как при этом обеспечивается более удобное производство строительных работ.
Для бетонных спиральных камер в практике отечественного турбиностроения угол охвата φСП = 180 ÷ 225°, чаще всего φСП = 180.
Выбор соотношений размеров m и n (рис. 7.5) определяется конструкцией подводной части гидроэлектростанции и турбинного оборудования. С точки зрения гидравлики нет препятствий к выбору любых соотношений m и n в пределах от m= b — b0 и n = 0 до m = 0 и n = b — b0.
При n = 0 спиральная камера получает развитие вниз относительно направляющего аппарата турбины. Это уменьшает объем бетона в массиве подводной части и освобождает пространство между перекрытием спиральной камеры и полом машинного зала, которое может быть использовано для вспомогательного оборудования гидроэлектростанции. При такой форме спиральной камеры, в частности, удобно размещаются шахты сервомоторов направляющего аппарата. Поэтому выгодно принимать n = 0, кроме тех случаев, когда подводная часть станции используется для водосбросных галерей. В этом случае сечение спиральной камеры должно развиваться вверх.

Рисунок 7.10. Тавровое сечение бетонной спиральной камеры
с плоским потолком, n = 0

 Необходимые при проектировании размеры диаметров расположения осей лопаток направляющего аппарата D0, входных Dа и выходных Db кромок статорных ребер (рис. 7.5 и 7.10) даны в таблице 7.3. Построив входное сечениеABGHDC (рис. 7.11), через которое пропускается расход QВХ со средней скоростью vC, переходят к определению положения в плане других сечений спирали.
Необходимые при проектировании размеры диаметров расположения осей лопаток направляющего аппарата D0, входных Dа и выходных Db кромок статорных ребер (рис. 7.5 и 7.10) даны в таблице 7.3. Построив входное сечениеABGHDC (рис. 7.11), через которое пропускается расход QВХ со средней скоростью vC, переходят к определению положения в плане других сечений спирали.
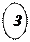 Рисунок 7.11. К расчету спиральных камер, имеющих радиальные сечения тавровой формы. Вершины наружных углов лежат на кривых AG и СН.
Рисунок 7.11. К расчету спиральных камер, имеющих радиальные сечения тавровой формы. Вершины наружных углов лежат на кривых AG и СН.
Изменение сечений производится закономерно, так, чтобы вершины наружных углов лежали на прямых AG и СН (рис. 7.11) или на кривых AG и СН (рис. 7.11). Обычно задают зависимость между размером а сечения и его высотой по параболическому закону, причём для части сечения, расположенной выше направляющего аппарата — по кубической параболе, а для части, расположенной ниже направляющего аппарата — по квадратичной параболе.
Таким образом:
для верхней части сечений: n = к1 ∙а3
для нижней части сечений: m = к2 ∙а2
Здесь коэффициенты к1 и к2 определяются по заданным размерам входного сечения: к1 = nВХ / а3ВХ; к2 = mВХ / а2ВХ.
Аналитический расчет спиральных камер с тавровыми радиальными сечениями. При простых формах радиальных сечений спиральной камеры, например с сечениями тавровой формы (рис.7.11) Ji может быть определен аналитически, а именно для любого сечения i:
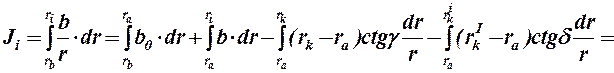
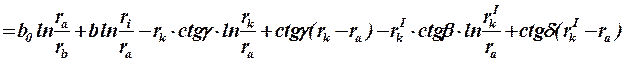
Здесь: m = ( rk – ra)ctgγ, и n = (rIk – ra)ctgδ, следовательно:
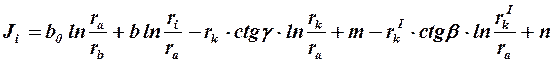
Для спиральных камер с плоским потолком n = 0 и rIk = ra, поэтому для них справедливо выражение:
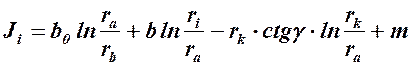
Задаваясь углом ri (как правило с шагом 0.3 ÷ 1.0 м) и расчитывая радиус φi можно изобразить зависимость φСП = f (Ri) и в конечном итоге построить очертание спиральной камеры.
В определение величины Ji входит постоянный член - 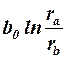 , остальные данные расчета сводятся в таблицу:
, остальные данные расчета сводятся в таблицу:
| Наименование величины | Сечения | ||
| 1 | … | i (конечное) | |
| Радиус ri, м | |||
| Высота b, м | |||
| rk, м | |||
| rk / rа | |||
| ln rk / rа | |||
| ri / rа | |||
| ln ri / rа | |||
| bln ri / ra | |||
| rk ctgγ, м | |||
| rk ctgγ ln rk / rа м | |||
| m, м | |||
| Ji | |||
| φi | |||
| Q м3 / с | |||
| F м2 | |||
| vСР |
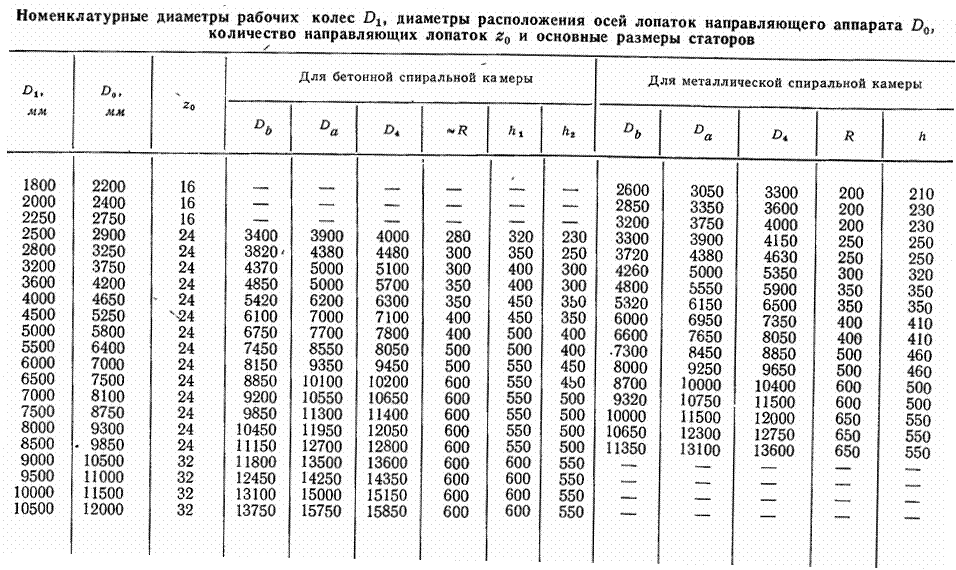 Таблица 7.3
Таблица 7.3
 2014-01-25
2014-01-25 897
897








