Сложное движение твердого тела

Рис.53

Рис.52

Рис.51

Если переносное движение подвижной систе­мы отсчета есть поступательное движение, то 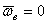и поэтому поворотное ускорение 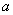точки также равно нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда 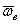в данный момент времени обращается в нуль.

Кроме того, поворотное ускорение точки может, очевидно, обращать­ся в нуль, если:

а) вектор относительной скорости 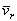точки параллелен вектору уг­ловой скорости 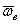переносного вращения, т.е. относительное движение точки происходит по направлению, параллельному оси переносного вращения;

б) точка не имеет движения относительно подвижной системы от­счета или относительная скорость 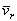точки в данный момент времени равна нулю ().

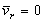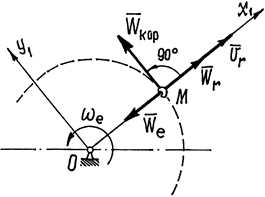
Пример 14. Пусть тело вращается вокруг неподвижной оси z. По поверхности его движется точка М (рис. 52). Конечно, скорость этого движения точки – относительная скорость 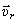, а скорость вращения тела – угловая скорость переносного движения .

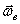Ускорение Кориолиса 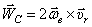, направлено перпен­дикулярно этим двум векторам, по правилу направления вектора век­торного произведения. Так, как пока­зано на рис. 52.

Нетрудно сформулировать более удобное правило определения направ­ления вектора 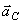: нужно спроектировать вектор относитель­ной ско­рости 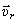на плоскость перпендикуляр­ную оси переносного вращения и за­тем повер­нуть эту проекцию на 90 градусов в плоскости по направлению переносного вращения. Конечное положение проекции вектора 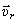укажет направление кориолисова ускорения. (Это правило было предложено Н.Е. Жуковским).

Пример 15. (Вернемся к примеру 13). Найдем абсолютное ускорение колечка М:

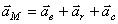. (6)

Переносное ускорение при движении колечка по окружности радиусом : 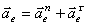, где .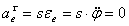

Значит 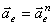(рис.53).

Относительное ускорение .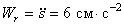

Ускорение Кориолиса .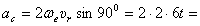

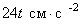Вектор 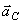направлен перпендикулярно стержню в сторону вращения (по правилу Жуковского).

Рис.10.7.

Величину абсолютного ускорения колечка М найдем с помощью проекций на подвижные ос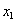и и 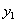проектируя равенство (6) на оси, получим: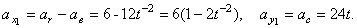

Тогда .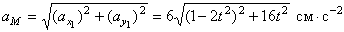

Так же как при сложном движении точки нередко и движение тела можно рассматривать как сумму нескольких движений. Например, со­стоящее из двух поступательных движений или поступательного движения и вращения в округ оси. Часто встречаются движения, состоящие из двух вращений вокруг осей или поступательного движения и вращения вокруг точки. Исследование движения точек принадлежащих телу, совершаю­щему сложное движение, можно проводить методами, изложенными выше и никаких особых трудностей не вызывает. Но анализ сложного движения тела, состоящего из нескольких вращений, обнаруживает неко­торые особенности, которые следует рассмотреть специально.