2014-01-25
824
Лекция 5
Краткое содержание: Скорости и ускорения точек тела при вращении. Векторные формулы для скоростей и ускорений точек тела. Сложное движение точки. Абсолютное, относительное и переносное движение точки. Сложение скоростей. Сложение ускорений при поступательном движении твердого тела.
Перейдем к изучению движения отдельных точек твердого тела. Известно уравнение вращения твердого тела вокруг неподвижной оси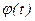 
.
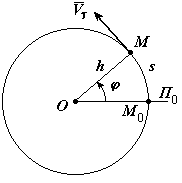Рассмотрим какою-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения. При вращении твердого тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр О лежит на самой оси. Если за время 
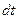происходит элементарный поворот тела на угол 
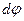, то точка М при этом совершает вдоль своей траектории элементарное перемещение 
.
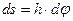Тогда алгебраическая скорость будет равна
или 
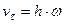(5-1)
Рис. 5-1
Скорость точки равна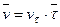 
. Скорость 
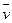в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью.
Модуль скорости равен
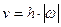. (5-2)
Величины скоростей точек тела, при его вращении вокруг неподвижной оси, пропорциональны кратчайшим расстояниям от этих точек до оси. Коэффициентом пропорциональности является угловая скорость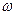 
. Скорости точек направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.
Ускорение точки раскладываем на касательную и нормальную составляющие, т.е.
.
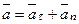Касательное и нормальное ускорения вычисляются по формулам
, 
.
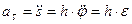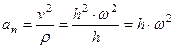Таким образом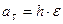 
, 
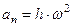и модуль ускорения вычисляется по формуле 
.
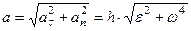Касательные, нормальные и полные ускорения точек тела, при его вращении вокруг неподвижной оси, как и скорости, так же пропорциональны кратчайшим расстояниям от этих точек до оси. Нормальное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от знака углового ускорения.
