Векторные скорости и ускорения точек тела

Скорость точки по модулю и направлению можно представить векторным произведением

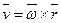, (5-3)

где 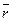- радиус-вектор точки М, проведенный из произвольной точки оси вращения .

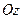Это выражение называется векторной формулой Эйлера.

Доказательство. Вектор 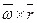перпендикулярен плоскости, в которой расположены векторы 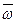и 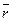, следовательно, по направлению он совпадает со скоростью 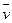. Модуль векторного произведения 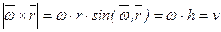Таким образом, векторное произведение 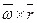по модулю и направлению определяет скорость точки.

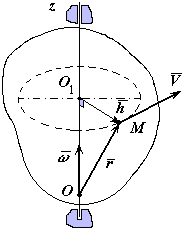
Рис. 5-2

Определим ускорение точки продифференцировав формулу Эйлера.

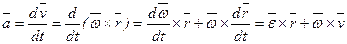, или

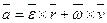
Первое слагаемое является касательным ускорением, а второе – нормальным.

.

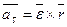
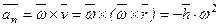Сопоставление двух формул для скорости точк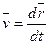и ( и 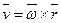) дает формулу для вычисления производной по времени от вектора :

.

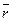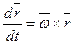В этой формуле вектор 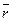имеет постоянный модуль, так как соединяет все время две точки твердого тела.