Потенциальная температура

Температура, которую примет воздушная частица, если ее опустить или поднять сухоадиабатически с исходного уровня до уровня, где давление равно 1000 гПа, носит название потенциальной температуры. Обозначим ее Q.

Рассмотрим два состояния воздушной частицы: начальное и конечное. Поскольку процесс адиабатический, то в соответствии с (8) 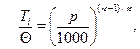или 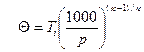. (16)

Нетрудно получить приближенное выражение для Q. Поскольку при опускании на каждые 100 м частица нагревается на 1°С, то при давлении на поверхности Земли р₀ =1000 гПа .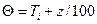

Потенциальная температура обладает очень важным свойством: при сухоадиабатических перемещениях одной и той же воздушной частицы она сохраняет постоянное значение. В самом деле, логарифмируя и дифференцируя (16), получаем: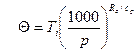

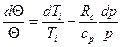. (17)

Согласно (9) правая часть уравнения (17) при адиабатическом процессе равна нулю. Таким образом, при адиабатическом движении воздушной частицы 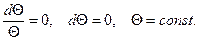(18)

Следовательно, если воздушная масса перемещается без теплообмена с окружающей средой (адиабатически), то ее потенциальная температура остается постоянной (в то время как Т изменяется). Это свойство сохранения (консервативности) потенциальной температуры используется в качестве характеристики воздушных масс. Если в процессе движения воздушной массы ее потенциальная температура изменилась, то это однозначно говорит о том, имел место приток или отток тепла. Сравнение уравнений (17) и (5) показывает, что приток тепла к воздушной частице связана с изменением ее температуры уравнением

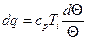(19) см.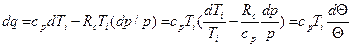

Если воспользоваться уравнением статики, то уравнению (17) можно придать вид

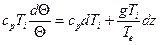, см.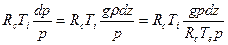

или

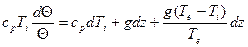. (20)

Введем следующие обозначения:

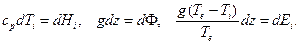
Здесь 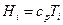– теплосодержание или энтальпия, 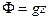– потенциальная энергия, 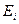– так называемая энергия неустойчивости. С учетом введенных обозначений

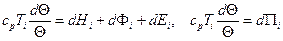(21)

где 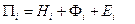- полная энергия частицы единичной массы.

Уравнение (21) показывает, что изменение потенциальной температуры однозначно связано с изменением полной энергии воздушной частицы. При адиабатическом перемещении частицы ее полная энергия не изменяется.