ЧАСТНЫЕ СЛУЧАИ ПРОСТРАНСТВЕННЫХ СИСТЕМ СИЛ.
- ИЗМЕНЕНИЕ ГЛАВНОГО МОМЕНТА ПРИ ПЕРЕМЕНЕ ЦЕНТРА ПРИВЕДЕНИЯ
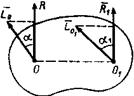
Пусть система сил приведена к центру O и получены в этой точке вектор 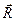 и главный момент
и главный момент 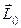 (рис. 24). Выберем в качестве цента приведения другую точку
(рис. 24). Выберем в качестве цента приведения другую точку 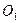 и вычислим момент рассматриваемой системы сил.
и вычислим момент рассматриваемой системы сил.
Силу 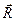 из
из 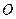 точки перенесем в точку
точки перенесем в точку 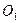 . Получим в этой точке силу
. Получим в этой точке силу 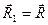 и, согласно теореме о параллельном переносе силы, присоединенную пару сил с векторным моментом
и, согласно теореме о параллельном переносе силы, присоединенную пару сил с векторным моментом 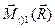 .
.
Векторный момент пары сил 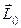 , вычисленный относительно точки
, вычисленный относительно точки  как вектор свободный, можно приложить в любой точке тела. Перенесем в точку
как вектор свободный, можно приложить в любой точке тела. Перенесем в точку 
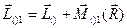
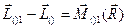
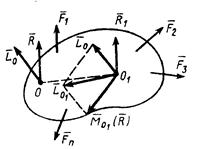
По формуле для векторного момента силы имеем
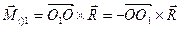
С учетом этого формула примет вид
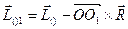
Итак, момент системы сил при перемене центра приведения изменяется на векторный момент главного вектора 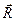 , приложенного старом центре приведения, относительно нового центра приведения
, приложенного старом центре приведения, относительно нового центра приведения 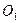 .
.
- Инвариантные системы сил
Инвариантамив статике называются такие величины для рассматриваемой системы сил, которые не изменяются при изменении центра приведения. Одним из инвариантов является главный вектор 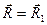

Главный вектор системы сил является векторным инвариантом. Для получения второго, скалярного, инварианта используем
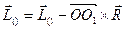
Умножая обе части этого равенства скалярно на 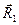 , причем в правой части при умножении вместо
, причем в правой части при умножении вместо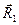 , возьмем
, возьмем 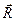 ,получим
,получим
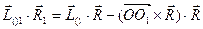 или
или
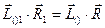 так как
так как 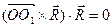
Скалярное произведение главного момента на главный вектор не зависит от центра приведения. Второй инвариант можно выразить в формуле:
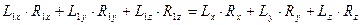
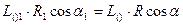
где 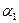 -угол между векторами
-угол между векторами 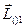 и
и 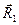 , а
, а 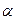 -между
-между 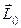 и
и 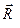 (рис. 25). После сокращения на
(рис. 25). После сокращения на 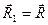 получим
получим
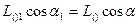
Проекция главного момента на направление главного вектора не зависит от центра приведения.
 2014-01-25
2014-01-25 815
815








