Уравнение центральной винтовой оси

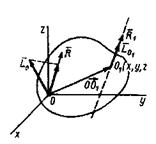
Предположим, что в центре приведения, принятом за начало координат, получены главный вектор 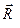с проекциями на оси координат 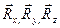и главный момент 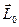с проекциями 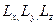При приведении системы сил к центру приведения О₁ (рис. 30) получается динама с главным вектором 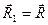и главным моментом 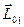, Векторы 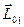и 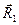как образующие линаму. параллельны и поэтому могут отличаться только скалярным множителем k_0. Имеем,, так как 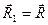. Главные моменты и 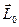, удовлетворяют соотношению

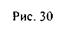
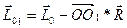
Подставляя 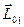, получим

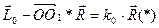
Координаты точки О₁ в которой получена динама, обозначим х, у, z. Тогда проекции вектора 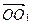на оси координат равны координатам х, у, z. Учитывая это, (*) можно выразить в форме

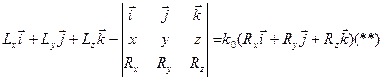
где i. j,k - единичные векторы осей координат, а векторное произведение 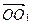*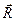представлено определителем. Векторное уравнение (**) эквивалентно трем скалярным, которые после отбрасывания 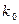можно представить в виде

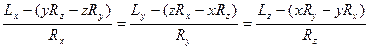
Полученные линейные уравнения для координат х, у, z являются уравнениями прямой линии - центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.

5. ЧАСТНЫЕ СЛУЧАИ ПРИВЕДЕНИЯ ПРОСТРАНСТВЕННОЙ