2014-01-25
1196
Произвольная система сил приводится к силе, равной главному вектору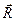 
, и паре сил, векторный момент которой равен главному моменту 
.
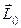Приведение к паре сил. Если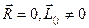 
, то система сил приводится к одной паре сил, причем главный момент в этом случае, не зависит от выбора центра приведения. В рассматриваемом случаи оба инварианта системы сил равны нулю, т.е.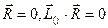 
Приведение к равнодействующей. Возможны два случая:
1. Если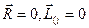 
(первый инвариант 
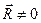, второй 
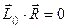),то система приводится к равнодействующей силе 
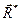, равной по модулю и направлению главному вектору 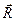, т. е. =
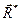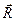
2. ,
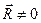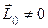, но 
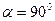,т.е.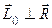 
(первый инвариант 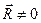, второй 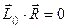), то система сил тоже приводится к равнодействующей, причем опять =
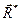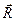
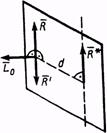
Но линия действия равнодействующей силы 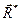отстоит от центра приведения на расстоянии 
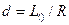(рис. 26)
 |
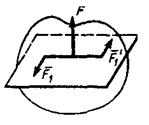Приведение к динаме. Динамой в механике называют такую совокупность силы 
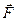и пары сил (
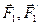) действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил (рис 27). Используя векторный момент 
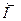пары сил 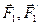, можно также определить динаму как совокупность силы и пары, у которы сила параллельна векторному моменту пары сил
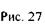Рассмотрим теперь случай, в котором 
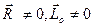и векторы 
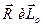не перпендикулярны. В этом случае оба инварианта не равны нулю, т. е.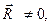 
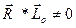
Покажем, что система сил в этом случае приводится к динаме, причем элементами динамы являются сила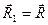 
и момент пары L1, = Lo COS α, где α - угол между векторами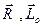 
Действительно, после приведения системы сил к центру О получим главный вектор R и главный момент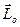 
. Косинус утла а между ними можно определить выражая скалярное произведение векторов 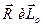в двух формах:
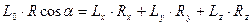
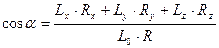
I
Разложим главный момент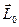 
на две взаимно перпендикулярные составляющие 
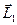и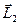 
, одна из
которых 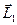направлена по главному вектору 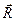(рис 28). Имеем
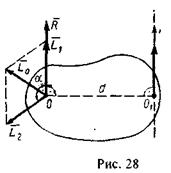
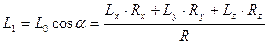
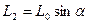
Векторный момент пары сил 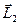перпендикулярен главному вектору 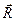. Такая система силы 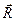и пары с моментом 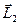приведется к одной силе 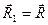, линия действия которой находится от точки О на расстоянии I
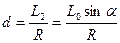
Рассматриваемая система сил заменилась эквивалентной системой сил. I
состоящей из силы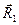 
и пары сил с векторным моментом 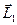, который как свободный вектор можно перенести из точки О в любую точку, в том числе и в точку О1 на линии действия силы 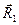. To есть
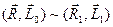
причем система сил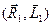 
является динамой. Сила и векторный момент пары 
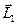есть элементы динамы:
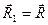
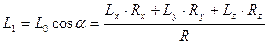
Линия, по которой направлена сила динамы,, называется центральной винтовой осью. Во всех точках винтовой оси, принятых за центры приведения, система сил приводится к одной и той же динаме. Расстояние от центра приведения О до центральной винтовой оси
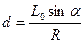
Если брать за центры приведения точки на поверхности цилиндра, осью которого является центральная винтовая ось, то главные моменты относительно таких центров будут одинаковы по модулю и составляют одинаковый угол с образующими цилиндра. Эти главные моменты состоят из одного и того же момента 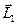входящего в состав динамы, и моментов 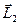перпендикулярных 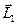и по числовой величине пропорциональных расстоянию центра приведения от центральной винтовой оси.
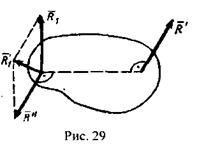
Совокупность сил, образующих динаму, можно заменить двумя скрещивающимися силами. Для этого следует одну из сил пары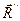 
совместить с точкой приложения силы 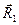и сложить с этой силой (рис. 29).
Рассмотрены все возможные случаи, кроме случая равновесия системы сил (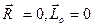
), рассмотренного ранее. Таким образом, убедились, что только при обращении в нуль главного вектора и главного момента система может находиться в равновесии, т. е. обращение в нуль главного вектора и главного момента не только необходимо для равновесия системы сил, но и достаточно.
