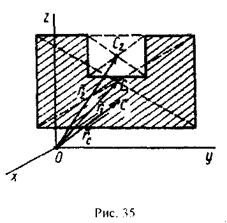
 Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 35). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 35). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 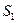 и центром масс C1 полностью заполнен массой (имеет положительную площадь). На той части фигуры, которую добавили, следует распределить отрицательную массу (отрицательную площадь) той же плотности. Площадь этой фигуры с отрицательной массой обозначим
и центром масс C1 полностью заполнен массой (имеет положительную площадь). На той части фигуры, которую добавили, следует распределить отрицательную массу (отрицательную площадь) той же плотности. Площадь этой фигуры с отрицательной массой обозначим 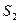 , а ее центр масс-С2. Применяя метод разбиения на части, радиус-вектор заданной фигуры определим по формуле:
, а ее центр масс-С2. Применяя метод разбиения на части, радиус-вектор заданной фигуры определим по формуле:
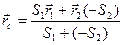
В отличие от обычного метода разбиения на части в формуле (2) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
• Основные понятия статики: материальная точка, механическая система,
абсолютно твердое тело, сила, система сил, эквивалентные системы сил,
равновесная система сил, равнодействующая сила, уравновешивающая
сила.
• Аксиомы статики. Теорема о переносе силы вдоль линии действия. Теорема
о трех силах.
• Система сходящихся сил. Равнодействующая сходящихся сил.
Геометрический и аналитический способы сложения сил. Условия
равновесия системы сходящихся сил.
• Моменты сил. Алгебраический и векторный момент силы относительно
точки. Момент силы относительно оси.
• Приведение силы к заданному центру. Основная теорема статики.
• Условия равновесия системы сил в векторной форме. Условия равновесия
пространственной системы сил в аналитической форме. Условия
равновесия пространственной и плоской систем параллельных сил. Три
формы условия равновесия плоской произвольной системы сил.
• Теоремы Вариньона. Инварианты системы сил. Частные случаи приведения
систем сил.
• Трение скольжения. Закон кулона. Угол и конус трения. Трение качения.
• Центр системы параллельных сил. Методы (симметрии, разбиения на части,
отрицательных масс) и формулы для вычисления центров тяжести.
• Теория пар сил. Пара сил и алгебраический момент пары сил. Теорема об
эквивалентности двух пар сил. Теорема о переносе пар сил в параллельную
плоскость. Векторный момент пары сил. Теорема о сумме моментов сил
пары. Сложение пар сил. Условия равновесия пар сил.
ЭКЗАМЕНАЦИОННЫЕ ЗАДАЧИ
1.2.16 Однородный шар 2 весом 36 Н опирается на ролики 1 и 3. Определить давление шара на ролик 1, если угол а = 45°. (25,5) 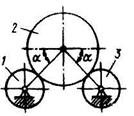 |
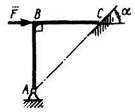 1.2.24 Изогнутый стержень ABC прикреплен к полу посредством шарнира А, а другой его конец С свободно опирается на гладкую поверхность, образующую угол а = 45°. Определить реакцию шарнира А, если на стержень действует сила F = 10 Н. (7,07) 1.2.24 Изогнутый стержень ABC прикреплен к полу посредством шарнира А, а другой его конец С свободно опирается на гладкую поверхность, образующую угол а = 45°. Определить реакцию шарнира А, если на стержень действует сила F = 10 Н. (7,07) |
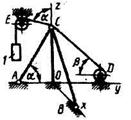 1.4.6 Для подъема тяжелых деталей применяется тренога АОСВ и лебедка D. Определить усилие в стержне АС, если вес поднимаемого груза 1 равен 60 Н, трос DСЕ лежит в плоскости Oyz, углы а = 60, β = 45°. (-19,1) 1.4.6 Для подъема тяжелых деталей применяется тренога АОСВ и лебедка D. Определить усилие в стержне АС, если вес поднимаемого груза 1 равен 60 Н, трос DСЕ лежит в плоскости Oyz, углы а = 60, β = 45°. (-19,1) |
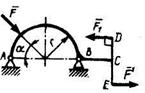 2.1.7 На арку ABC действуют пара сил 2.1.7 На арку ABC действуют пара сил 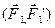 и сила F = 2 Н. Определить сумму их моментов относительно точки В, если сила F1 = 3 Н, радиус г = 1 м, плечо DE = 1,2 м, угол а = 45°. (5.01). и сила F = 2 Н. Определить сумму их моментов относительно точки В, если сила F1 = 3 Н, радиус г = 1 м, плечо DE = 1,2 м, угол а = 45°. (5.01). |
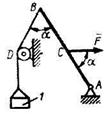 2.1.10 К стержню АВ. закрепленному в шарнире А, привязана веревка BD с грузом 1. Определить силу F, необходимую для того, чтобы удержать стержень в равновесии, если угол а = 60°. вес груза 2 Н, расстояние АС = ВС. (4,0) 2.1.10 К стержню АВ. закрепленному в шарнире А, привязана веревка BD с грузом 1. Определить силу F, необходимую для того, чтобы удержать стержень в равновесии, если угол а = 60°. вес груза 2 Н, расстояние АС = ВС. (4,0) |
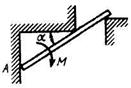 2.4.19 Стержень удерживается под углом а = 30° к горизонту. Определить реакцию опоры А, если момент пары сил М= 25 кН • м. (0) 2.4.19 Стержень удерживается под углом а = 30° к горизонту. Определить реакцию опоры А, если момент пары сил М= 25 кН • м. (0) |
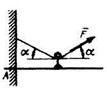 2.4.40 Определить в кН горизонтальную составляющую реакции в заделке А консольной балки, если сила натяжения троса F = 25 кН, угол а = 30°. (0) 2.4.40 Определить в кН горизонтальную составляющую реакции в заделке А консольной балки, если сила натяжения троса F = 25 кН, угол а = 30°. (0) |
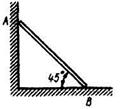 2.5.4 Однородный брус АВ опирается в точке А на гладкую стену, а в точке В на негладкий пол. Определить наименьший коэффициент трения скольжения между брусом и полом, при котором брус останется в указанном положении в покое. (0,50) 2.5.4 Однородный брус АВ опирается в точке А на гладкую стену, а в точке В на негладкий пол. Определить наименьший коэффициент трения скольжения между брусом и полом, при котором брус останется в указанном положении в покое. (0,50) |
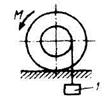 2.6.12 К однородному катку, малый радиус которого 0,2 м, подвешен груз 1 весом 200 Н и приложена пара сил с моментом М = 57.6 Н•м. Определить в кН наибольший вес катка, при котором он будет катиться влево, если коэффициент трения качения δ= 0,008 м. (2.0) 2.6.12 К однородному катку, малый радиус которого 0,2 м, подвешен груз 1 весом 200 Н и приложена пара сил с моментом М = 57.6 Н•м. Определить в кН наибольший вес катка, при котором он будет катиться влево, если коэффициент трения качения δ= 0,008 м. (2.0) |
3.1.9 Укажите номер статически неопределимой системы. (3) 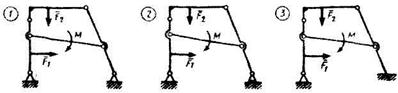 |
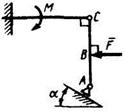 3.2.5 Определить реакцию опоры А в кН, если сила F = 3 кН, угол а = 30°, размеры АВ = ВС. (3) 3.2.5 Определить реакцию опоры А в кН, если сила F = 3 кН, угол а = 30°, размеры АВ = ВС. (3) |
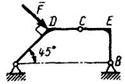 3.2.11 Определить вертикальную составляющую реакции в шарнире В, если сила F = 850 Н, а размеры DC = СЕ = BE. (401) 3.2.11 Определить вертикальную составляющую реакции в шарнире В, если сила F = 850 Н, а размеры DC = СЕ = BE. (401) |
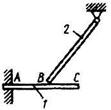 3.2.19 Однородный брус 2 весом 400 Н свободно опирается в точке В на однородную балку 1. Чему должен равняться вес балки 1, для того чтобы момент в заделке А был равен 265Нм, если размеры АВ = 1 м, ВС = 0,8 м. (72,2) 3.2.19 Однородный брус 2 весом 400 Н свободно опирается в точке В на однородную балку 1. Чему должен равняться вес балки 1, для того чтобы момент в заделке А был равен 265Нм, если размеры АВ = 1 м, ВС = 0,8 м. (72,2) |
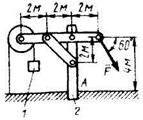 3.2.29 Определить в кН модуль силы F, при которой момент в заделке А столба 2 равен нулю, если вес тела 1 равен 10 кН. Весом остальных элементов конструкции пренебречь. (21,4) 3.2.29 Определить в кН модуль силы F, при которой момент в заделке А столба 2 равен нулю, если вес тела 1 равен 10 кН. Весом остальных элементов конструкции пренебречь. (21,4) |
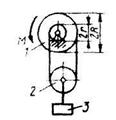 3.3.2 Определить момент M пары сил, который необходимо приложить к барабану 1 дифференциального ворота для равномерного подъема груза 3 весом 2 • 103 Н. если радиусы R = 15 см и r = 10 см. Весом блока 2 пренебречь. (50) 3.3.2 Определить момент M пары сил, который необходимо приложить к барабану 1 дифференциального ворота для равномерного подъема груза 3 весом 2 • 103 Н. если радиусы R = 15 см и r = 10 см. Весом блока 2 пренебречь. (50) |
3.3.3 На звено ВС шарнирного четырехзвенника действует пара сил с моментом М2 = 200 Н • м. Определить момент М, пары сил, который надо приложить к кривошипу ОА, для того чтобы механизм находился в равновесии, если длины звеньев ВС = 2ОА = 400 мм. (100) 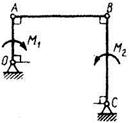 |
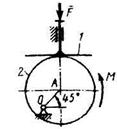 3.3.5 На толкатель 1 кулачкового механизма действует сила F = 100 Н. При каком моменте М пары сил, приложенных к кулачку 2, возможно равновесие механизма, если расстояние ОА = 10 см. (7,07) 3.3.5 На толкатель 1 кулачкового механизма действует сила F = 100 Н. При каком моменте М пары сил, приложенных к кулачку 2, возможно равновесие механизма, если расстояние ОА = 10 см. (7,07) |
3.3.8 Кривошипно-ползунный механизм находится в равновесии. Определить в кН силу взаимодействия кривошипа ОАС и шатуна АВ, если к точке С приложена вертикальная сила F1 = 1 кН, размеры ОА = АС = 0,3 м, угол а = 45°. (1,41)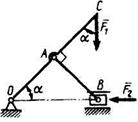 |
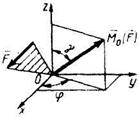 |
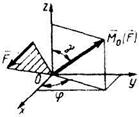 5.1.4 Момент силы F, относительно центра О равен М0 (F)= 100 Н•м и расположен в пространстве так, что утлы γ = 30° и φ = 30°. Определить момент этой силы относительно оси Оy: (25) 5.1.4 Момент силы F, относительно центра О равен М0 (F)= 100 Н•м и расположен в пространстве так, что утлы γ = 30° и φ = 30°. Определить момент этой силы относительно оси Оy: (25) |
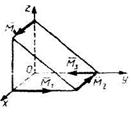 5.2.6 Определить модуль момента уравновешивающей пары сил для пространственной системы четырех пар сил, если М1=М2 = М3 = М4 =20 Н • м. (0) 5.2.6 Определить модуль момента уравновешивающей пары сил для пространственной системы четырех пар сил, если М1=М2 = М3 = М4 =20 Н • м. (0) |
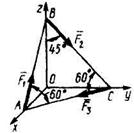 5.3.12 Тетраэдр О ABC находится под действием сил F1= F2= F3=10H. Приняв за центр приведения точку В, определить модуль главного момента этих сил, если длина ребер АВ = ВС = АС = 2м. (17,3) 5.3.12 Тетраэдр О ABC находится под действием сил F1= F2= F3=10H. Приняв за центр приведения точку В, определить модуль главного момента этих сил, если длина ребер АВ = ВС = АС = 2м. (17,3) |
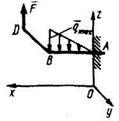 5.4.6 На участке АВ II Ох изогнутой балки ABD действует распределенная нагрузка интенсивностью qmax = 20 Н/м. К точке D балки приложена сила F=10 Н. Определить главный вектор данной системы сил, если АВ = 3 м, a BD перпенд. АВ и BD II Оу. (20) 5.4.6 На участке АВ II Ох изогнутой балки ABD действует распределенная нагрузка интенсивностью qmax = 20 Н/м. К точке D балки приложена сила F=10 Н. Определить главный вектор данной системы сил, если АВ = 3 м, a BD перпенд. АВ и BD II Оу. (20) |
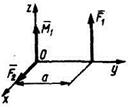 5.4.15 Определить угол между главным вектором и моментом данной системы сил, принимая за центр приведения точку О, если расстояние а=1м, момент пары сил М1= 1 Н • м, сила F1=F2= 1 H. (0) 5.4.15 Определить угол между главным вектором и моментом данной системы сил, принимая за центр приведения точку О, если расстояние а=1м, момент пары сил М1= 1 Н • м, сила F1=F2= 1 H. (0) |
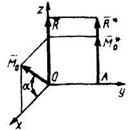 5.4.23 К невесомой пластине OABD приложены силы F1,F2 и F3, которые параллельны оси Оz причем сила F3= 2F1 = 2F2 = 2Н. Определить расстояние, при котором возможно равновесие системы сил, если расстояния b = 2 м, c= 1 м. (1) 5.4.23 К невесомой пластине OABD приложены силы F1,F2 и F3, которые параллельны оси Оz причем сила F3= 2F1 = 2F2 = 2Н. Определить расстояние, при котором возможно равновесие системы сил, если расстояния b = 2 м, c= 1 м. (1) |
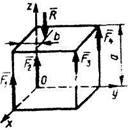 5.5.3 К кубу приложены силы F1,F2, F3 и F4, которые уравновешены силой R. Определить расстояние b силы R от плоскости Охz, если ребро куба а = 1 м, F1 = F2 = 15 Н, F3 = F4 = 5 Н и R = 40 Н. (0,25) 5.5.3 К кубу приложены силы F1,F2, F3 и F4, которые уравновешены силой R. Определить расстояние b силы R от плоскости Охz, если ребро куба а = 1 м, F1 = F2 = 15 Н, F3 = F4 = 5 Н и R = 40 Н. (0,25) |
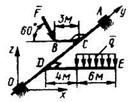 5.6.3 К валу ОА под прямым углом прикреплены стержни ВС и DE. К стержню DE приложена распределенная нагрузка q = 0,5 Н/м. Определить модуль силы F, уравновешивающей данную нагрузку, если F || Oxz. (8,08) 5.6.3 К валу ОА под прямым углом прикреплены стержни ВС и DE. К стержню DE приложена распределенная нагрузка q = 0,5 Н/м. Определить модуль силы F, уравновешивающей данную нагрузку, если F || Oxz. (8,08) |
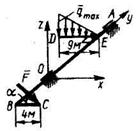 5.6.4 К валу АОВ под прямым утлом прикреплены стержень DE, несущий распределенную нагрузку qmax = 0,5 Н/м, и стержень ВС. Нагрузка уравновешивается силой F || Oxz, приложенной к точке С под углом а = 30°. Определить модуль этой силы. (6,75) 5.6.4 К валу АОВ под прямым утлом прикреплены стержень DE, несущий распределенную нагрузку qmax = 0,5 Н/м, и стержень ВС. Нагрузка уравновешивается силой F || Oxz, приложенной к точке С под углом а = 30°. Определить модуль этой силы. (6,75) |
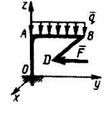 5.6.12 Фигурная балка OABD находится в равновесии. Определить составляющую в тоннах реакции заделки вдоль оси Oz, если дано: ОА = 1,7 м, АВ = 2 м, BD = 3,4 м, BD || Ох, сила F = 1 т и интенсивность распределенной нагрузки q = 2 т/м. (4) 5.6.12 Фигурная балка OABD находится в равновесии. Определить составляющую в тоннах реакции заделки вдоль оси Oz, если дано: ОА = 1,7 м, АВ = 2 м, BD = 3,4 м, BD || Ох, сила F = 1 т и интенсивность распределенной нагрузки q = 2 т/м. (4) |
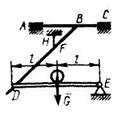 5.7.4 Однородная горизонтальная балка DE. на которой установлен груз весом G = 800 Н. в точке D опирается на горизонтальную стержневую конструкцию ABCD, удерживаемую вертикальным тросом FH. Определить реакцию подшипника А, если расстояния DF = 2FB, АВ = ВС. (400) 5.7.4 Однородная горизонтальная балка DE. на которой установлен груз весом G = 800 Н. в точке D опирается на горизонтальную стержневую конструкцию ABCD, удерживаемую вертикальным тросом FH. Определить реакцию подшипника А, если расстояния DF = 2FB, АВ = ВС. (400) |
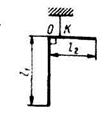 6.1.4 Однородная проволока, согнутая под прямым углом, подвешена, как показано на рисунке. Определить отношение L1||L2, при котором отрезок длиной l2 будет находиться в горизонтальном положении, если ОК = 0.2L2. (1.5) 6.1.4 Однородная проволока, согнутая под прямым углом, подвешена, как показано на рисунке. Определить отношение L1||L2, при котором отрезок длиной l2 будет находиться в горизонтальном положении, если ОК = 0.2L2. (1.5) |
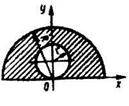 6.2.9 Определить координату центра тяжести у заштрихованной площади фигуры, если даны радиусы окружностей: R= 0,99 м, r = 0,33 м. (0,446) 6.2.9 Определить координату центра тяжести у заштрихованной площади фигуры, если даны радиусы окружностей: R= 0,99 м, r = 0,33 м. (0,446) |
 2014-01-25
2014-01-25 1239
1239
