Метод разбиения на части (метод группировки)

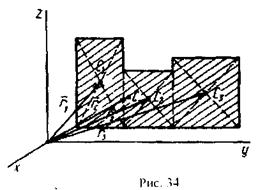
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные ча­сти, на которые оно разбито. Покажем это на частном примере плоской фигуры (рис. 34). Плоскую фигуру можно разбить на три части, центры тяжести которых С₁, С₂, С₃ известны. Они находятся на пересечении диагоналей прямоугольников. 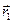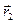Их радиусы – векторы обозначим 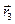и площади S₁, S₂, S3. Общая площадь сложной фигуры будет S = S₁ + S₂ + S₃.

Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим

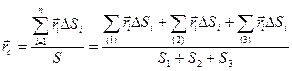
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:

, ,

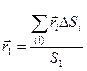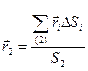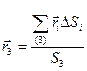
Или

, ,

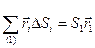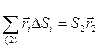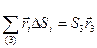
Используя эти формулы для радиуса-вектора всей фигуры, имеем

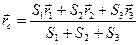(1)

Полненная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.