Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами статики. Аксиомы статики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой.
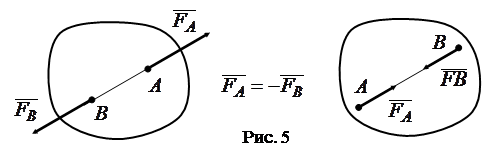 |
Аксиома 1. Под действием двух сил твердое тело находится в равновесии тогда и только тогда, когда эти силы прямо противоположны, то есть равны по величине, направлены в противоположные стороны и имеют общую линию действия (рис. 5).
Аксиома 2. Равновесие твердого тела не нарушится, если к силам, действующим на тело, присоединить, либо из числа сил, действующих на тело, изъять, если таковые имеются, две прямо противоположные силы.
Следствие 1. Равновесие твердого тела не нарушится, если любую из сил, приложенных к телу, перенести вдоль ее линии действия.
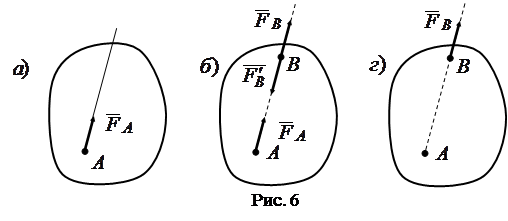 |
Действительно, пусть сила
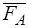 приложена в точке
приложена в точке 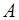 (рис. 6а).
(рис. 6а).
Приложим в произвольной точке 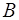 на линии действия
на линии действия 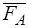 две прямо противоположные силы
две прямо противоположные силы 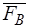 и
и 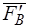 полагая, что
полагая, что 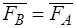 и
и 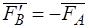 (рис. 6б). Согласно аксиоме 2 состояние равновесия не нарушится. Так как силы
(рис. 6б). Согласно аксиоме 2 состояние равновесия не нарушится. Так как силы 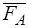 и
и 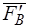 прямо противоположны, то, согласно аксиоме 2, их можно отбросить (рис. 6в). Вместо силы
прямо противоположны, то, согласно аксиоме 2, их можно отбросить (рис. 6в). Вместо силы 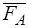 , приложенной в точке
, приложенной в точке 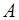 , осталась равная ей сила
, осталась равная ей сила 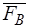 , приложенная в точке
, приложенная в точке 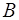 , что доказывает следствие. Это следствие показывает, что сила, приложенная к абсолютно твердому телу, представляет собой скользящий вектор. Полученный результат справедлив только для сил, действующих на абсолютно твердое тело; во всех других случаях (например, в случае деформируемых тел) сила, как было сказано выше, есть приложенный вектор.
, что доказывает следствие. Это следствие показывает, что сила, приложенная к абсолютно твердому телу, представляет собой скользящий вектор. Полученный результат справедлив только для сил, действующих на абсолютно твердое тело; во всех других случаях (например, в случае деформируемых тел) сила, как было сказано выше, есть приложенный вектор.
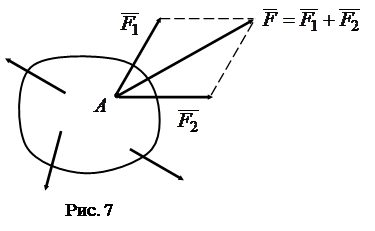 |
Аксиома 3. Равновесие твердого тела нарушится, если две силы, приложенные к одной его точке, заменить одной силой, приложенной в той же точке и равной их геометрической сумме (по правилу параллелограмма), либо одну силу заменить двумя ее составляющими (по тому же правилу).
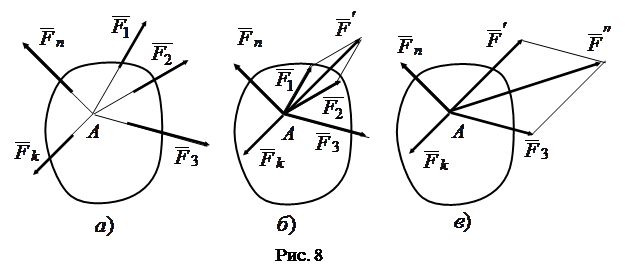 |
Следствие 2. Равновесие твердого тела не нарушится, если действующую на него систему сходящихся сил заменить одной силой, которая приложена в точке схода и равна главному вектору этой системы сил.
Согласно следствию 1, не нарушая равновесие тела, переносим силы 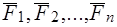 вдоль их линий действия в точку схода
вдоль их линий действия в точку схода 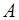 (рис. 8б), а затем по аксиоме 3 заменяем по правилу параллелограмма силы
(рис. 8б), а затем по аксиоме 3 заменяем по правилу параллелограмма силы 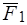 и
и 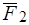 одной силой
одной силой 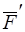 . Рассматриваемое тело находится в равновесии под действием приложенных в точке
. Рассматриваемое тело находится в равновесии под действием приложенных в точке 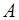 сил
сил 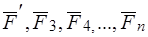 , то есть под действием
, то есть под действием 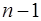 силы (рис. 8в). Снова применяем правило параллелограмма к двум силам
силы (рис. 8в). Снова применяем правило параллелограмма к двум силам 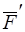 и
и 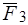 , заменяя их силой
, заменяя их силой 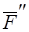 . Тело будет находиться в равновесии под действием
. Тело будет находиться в равновесии под действием 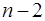 сил
сил 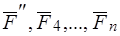 . Продолжая этот процесс до полного исчерпывания сил системы, получаем в результате только одну силу
. Продолжая этот процесс до полного исчерпывания сил системы, получаем в результате только одну силу 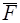 , приложенную в точке схода
, приложенную в точке схода 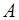 и заменяющую исходную систему сходящихся сил. Эта сила
и заменяющую исходную систему сходящихся сил. Эта сила 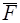 изображается главным вектором системы, так как нахождение геометрической суммы с помощью правила многоугольника и последовательным применением правила параллелограмма дает один и тот же результат.
изображается главным вектором системы, так как нахождение геометрической суммы с помощью правила многоугольника и последовательным применением правила параллелограмма дает один и тот же результат.
Следствие 3. Под действием одной силы тело не может находиться в состоянии равновесия.
Для доказательства разложим эту силу на две составляющие по правилу параллелограмма. Эти составляющие не прямо противоположны, следовательно, на основании аксиомы 1 тело не будет находиться в состоянии равновесия.
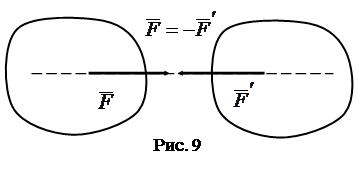 |
Аксиома 4 (третий закон Ньютона) Источником каждой силы является материальное тело, причем два тела действуют друг на друга с прямо противоположными силами.
Следует помнить, что силы действия 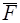 и противодействия
и противодействия 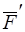 приложены к разным материальным телам.
приложены к разным материальным телам.
Аксиома 5 (принцип отвердевания). Состояние равновесия изменяемого(деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим(абсолютно твердым).
 2014-01-25
2014-01-25 848
848








