1. ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ЦЕНТРОВ ТЯЖЕСТИ.
Центром тяжести тела называют центр системы параллельных сил. которую приближенно образуют силы тяжести его элементарных частиц.
Радиус-вектор центра тяжести тела 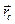 вычисляем как радиус-вектор центра параллельных сил по формуле:
вычисляем как радиус-вектор центра параллельных сил по формуле:
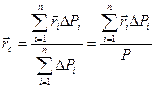 (1)
(1)
где 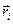 - радиус-вектор точки приложения силы тяжести элементарной части тела, принятой за точку;
- радиус-вектор точки приложения силы тяжести элементарной части тела, принятой за точку; 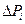 - сила тяжести элементарной частицы;
- сила тяжести элементарной частицы; 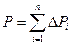 , - сила тяжести всего тела; n-число частей, на которое мысленно разбито все тело. Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести отдельных его частей считать системой параллельных сил.
, - сила тяжести всего тела; n-число частей, на которое мысленно разбито все тело. Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести отдельных его частей считать системой параллельных сил.
Если в (1) перейти к пределу, увеличивая число элементарных частей n до бесконечности, то после замены 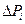 дифференциалом dP, а суммы - интегралом получим:
дифференциалом dP, а суммы - интегралом получим:
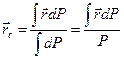 (1’)
(1’)
где 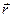 - радиус-вектор элементарной части тела, принятой за точку. В проекциях на оси координат из (1) и (1’) получаем:
- радиус-вектор элементарной части тела, принятой за точку. В проекциях на оси координат из (1) и (1’) получаем:
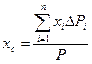 ,
, 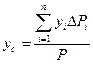 ,
, 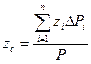 ,
,
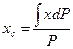 ,
, 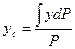 ,
, 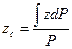
где 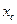 ,
,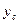 ,
,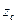 - координаты центра тяжести:
- координаты центра тяжести: 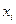 ,
,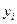 ,
,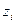 - координаты точки приложения силы тяжести
- координаты точки приложения силы тяжести 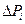 Используя понятие центр тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела можно выразить через их массы
Используя понятие центр тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела можно выразить через их массы 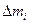 . и М и ускорение силы тяжести g с помощью формул
. и М и ускорение силы тяжести g с помощью формул
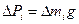
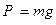
Подставляя эти значения сил тяжести в (1) и (1*) после сокращения на g, которое принимаем одинаковым для всех частей тела, имеем
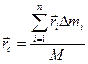 (2) И соответственно
(2) И соответственно 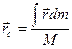 (1’)
(1’)
По формулам (2) и (2’) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор которой вычисляется по формулам (2) или (2'). В проекциях на оси координат из (2) и (2') получаем:
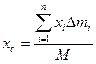 ,
, 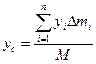 ,
, 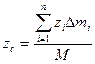 ,
,
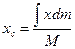 ,
, 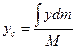 ,
, 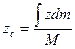
где 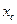 ,
,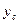 ,
,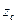 ‑ координаты центра масс тела.
‑ координаты центра масс тела.
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
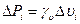 ,
, 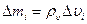
где 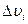 - объем элементарной частицы тела;
- объем элементарной частицы тела; 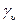 и
и 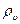 - соответственно удельный вес и плотность тела. Сила тяжести и масса всего тела
- соответственно удельный вес и плотность тела. Сила тяжести и масса всего тела
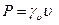 ,
, 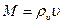
где 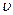 - объем тела. Подставляя эти значения в (2) и (2'), после сокращения на
- объем тела. Подставляя эти значения в (2) и (2'), после сокращения на 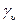 и
и 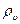 соответственно получим формулы
соответственно получим формулы
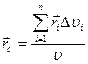 ,
, 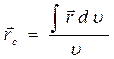
по которым определяют центр тяжести объёма тела.
Если тело имеет форму поверхности, т.е. один из размеров мал по сравнению с двумя другими, как, например, у гонкого листа железа, то имеем
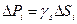 ,
, 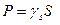
где 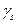 - удельный вес:
- удельный вес:  - площадь элементарной частицы поверхности; S-площадь всей поверхности. После сокращения на
- площадь элементарной частицы поверхности; S-площадь всей поверхности. После сокращения на 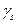 для однородной поверхности получим следующие формулы для определения центра тяжести ее площади:
для однородной поверхности получим следующие формулы для определения центра тяжести ее площади:
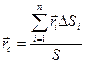 ,
, 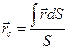
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
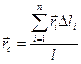 ,
, 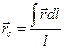
где 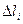 - длина элемента линии:
- длина элемента линии:  - общая длина линии, центр тяжести которой определяется.
- общая длина линии, центр тяжести которой определяется.
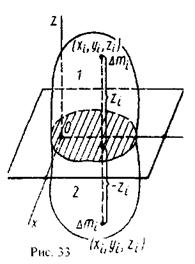 2. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЦЕНТРОВ ТЯЖЕСТИ (ЦЕНТРОВ МАСС)
2. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЦЕНТРОВ ТЯЖЕСТИ (ЦЕНТРОВ МАСС)
 2014-01-25
2014-01-25 885
885








