2018-02-13
419
Вільні коливання динамічної системи з n ступенями вільності описуються системою n лінійних однорідних диференціальних рівнянь другого порядку з постійними коефіцієнтами:
(3.1)
При умові, що точкові маси системи здійснюють гармонійні коливання, розв’язок системи (3.1) має вигляд
(3.2)
Після підстановки (3.2) в (3.1) і скорочення на 
одержимо систему однорідних алгебраїчних рівнянь відносно невідомих амплітуд переміщень точкових мас (
):
, (3.3)
де 
; 
– і -та колова частота власних коливань; 
– амплітуда коливань n -ої маси з і -тою частотою.
У матричній формі система рівнянь динамічної рівноваги (3.3) має вигляд
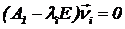, (3.4)
де 
; 
; 
;
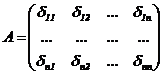m1, m2, …, mn – точкові маси системи;
Е – одинична матриця; А – матриця податливості;
– статичне переміщення і -тої маси від k -тої одиничної сили
(і = 1, 2, 3,…, n; k = 1, 2, 3,…, n);
– і -те власне число матриці А1 (і = 1,2,3,…,n);
– і -тий власний вектор матриці А1; 
.
Для того, щоб система (3.4) мала розв’язок (проблема власних значень), який відрізняється від нульового (
), необхідно, щоб головний визначник системи (4) дорівнював нулю:
|
|
|
. (3.5)
Рівняння (3.5) називають характеристичним (частотним або віковим) рівнянням вільних коливань.
Для пружної системи, стійкої в стані спокою, рівняння (3.5) має в загальному випадку n дійсних коренів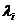 
(і = 1, 2, 3, …, n).
Ряд чисел 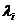і частот , розташованих у порядку зростання частот (зменшення 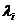), називається спектром власних чисел 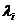і власних частот , а їм відповідає спектр форм власних коливань системи з n ступенями вільності.
Оскільки система (3.4) однорідна, то із неї може бути визначено лише співвідношення між компонентами 
. Якщо визначник системи (3.5) дорівнює нулю, то це означає, що залежність між рівняннями системи (3.4) – лінійна. Один із компонентів приймаємо за одиницю, після чого відповідний стовпець у системі (3.4) перетворюється в стовпець вільних членів. Із n рядків системи (3.4) вибирають будь-які n-1, що утворюють систему неоднорідних алгебраїчних рівнянь відносно інших n-1 компонентів вектора.
Таким чином розв’язавши систему алгебраїчних рівнянь n-1 порядку (попередньо обчисливши визначник (3.5), тобто визначивши значення частот вільних коливань) n разів, обчислюють відповідні головні форми коливань. Але це досить трудомісткий і роздільний процес. Існують інші методи розв’язання таких задач. В основному всі вони зводяться до визначення власних чисел і відповідних їм власних векторів для співвідношення
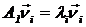. (3.6)
Для визначення власних чисел 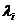і відповідних їм власних векторів досить зручним є метод ітерацій у сполученні з методом вичерпувань.
|
|
|
Задаючись довільним вектором 
на нульовій ітерації, наприклад:
,
підставляємо його в ліву частину виразу (3.6) й одержуємо
,
де 
– перше наближення старшого власного числа 
; 
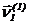– перше наближення вектора (перша форма коливань), координата 
якого дорівнює 1.
Підставляючи в ліву частину виразу (3.6) 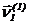, одержимо 
, 
і т. д. Процес ітерації закінчується, коли 
, де 
– наперед задана точність обчислень.
Методом ітерацій можна визначити лише перше власне число 
та відповідний власний вектор 
. Для одержання 
і 
необхідно одержати матрицю А2, що буде мати такі ж власні числа й вектори, як і матриця А1, за винятком та , котрі будуть дорівнювати нулю.
Останнє дає можливість до матриці А2 застосувати метод ітерацій та знайти та і т. д.
Матриця А2 визначається згідно з виразом (3.7) за методом вичерпування:
, (3.7)
де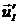 
– транспонований у матрицю-рядок власний вектор матриці 
, котрий визначають методом ітерацій. При цьому вектори 
і 
повинні бути нормовані так, щоб 
, тобто
; 
.
Послідовне використання виразу (3.7) дає можливість знайти всі власні числа та відповідні їм власні вектори матриці А1, тобто значення частот і відповідні їм форми вільних коливань.
За наведеною вище методикою був розроблений алгоритм і програма для ПЕОМ, яка дає можливість одержати частоти та відповідні їм форми вільних коливань динамічної системи з n ступенями вільності методами ітерацій і вичерпування. При цьому необхідно відмітити, що яке б власне число 
ми не приймали за початкове із власного вектора матриці А1, то в кінцевому результаті спектр частот залишається таким самим, а форми коливань взаємно ортогональними.
Питання для самоконтролю.
1. Задачі та методи динаміки стержневих систем (споруд).
2. Ступінь вільності динамічної системи та методи розрахунку її на дію динамічного навантаження.
3. Виконайте розрахунок вільних коливань динамічної системи з одним ступенем вільності без урахування й з урахуванням сил опору. Вкажіть основні механічні характеристики системи при коливаннях та вплив початкових умов.
4. Виконайте розрахунок вимушених коливань динамічної системи з одним ступенем вільності без урахування та з урахуванням сил опору. Поясніть зміст коефіцієнта динамічності та його залежність від сил опору.
5. Виконайте розрахунок вільних коливань динамічної системи з n ступенями вільності. Складіть частотне (вікове) рівняння, визначте спектр частот вільних коливань.
6. Матрична форма частотного рівняння. Визначення власних чисел та векторів, їх використання.
7. Головні форми коливань та їх властивості.
8. Одержання характеристик головних форм.
9. Виконайте розрахунок вимушених коливань динамічної системи з n ступенями вільності без урахування сил опору. Визначення коефіцієнтів динамічності.
10. Виконайте розкладання збурюючих сил за головними формами коливань. Розрахунок динамічних систем при резонансі.
11. Наведіть заходи боротьби зі шкідливими коливаннями.
ЛІТЕРАТУРА
Основна
1. Строительная механика. Динамика и устойчивость сооружений / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. - М.: Стройиздат, 1984. - 415 с.
2. Киселев, В.А. Строительная механика. Специальный курс. – 3-е изд., исправ. и доп. / В.А. Киселев. - М.: Стройиздат, 1980. - 616 с.
3. Строительная механика стержневых систем и оболочек / Ю.И. Бутенко, С.Н. Кан, В.П. Пустовойтов, и др.. - К.: Вища школа, 1980. - 488 с.
4. Дарков, А.В. Строительная механика. - 8-е изд., перераб. и доп. / А.В. Дарков, Н.Н. Шапошников. - М.: Высшая школа, 1986. - 600 с.
5. Дарков, А.В. Строительная механика. - 7-е изд., перераб. и доп. / А.В. Дарков, Н.Н. Шапошников. - М.: Высшая школа, 1976. - 599 с.
|
|
|
6. Баженов, В.А. Будівельна механіка. Комп’ютерні технології: підручник / В.А. Баженов, А.В. Перельмутер, О.В. Шишов. – К.: Каравела, 2009. – 696 с.
7. Баженов, В.А. Будівельна механіка: розрахункові вправи. Задачі. Комп’ютерне тестування: навч. посібник / В.А. Баженов, Г.М. Іванченко, О.В. Шишов. – К.: Каравела, 2006. – 344 с.
Допоміжна
8. Строительная механика. Руководство к практическим занятиям / под ред. Ю.И. Бутенко. - К.: Вища шк., 1989. - 367 с.
9. Безухов, Н.И. Устойчивость и динамика сооружений в примерах и задачах. – 3-е изд., перераб. и доп. / Н.И. Безухов, О.В. Лужин, Н.В. Колкунов. – М.: Высшая школа, 1987.–264 с.
10. Ржаницын, А.Р. Строительная механика / А.Р. Ржаницын. - М.: Высшая школа, 1982. -400 с.
11. Ржаницын, А.Р. Строительная механика / Ржаницын А.Р. – 2-е изд., перераб. и доп. - М.: Высшая школа, 1991. - 439 с.
12. Руководство к практическим занятиям по курсу строительной механики (основы теории устойчивости, динамики сооружений и расчета пространственных систем) / под ред. Г.К. Клейна. - 2-е изд., перераб. и доп. - М.: Высшая школа, 1972. - 320 с.
Додаток А
Формули для розрахунку стержневих систем на стійкість форми рівноваги методом переміщень у розгорнутій формі
