Задание № 1
Пример 1. Вычислить определитель 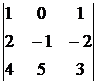 .
.
Решение. Вычислим определитель, используя правило треугольника

Пример 2. Вычислить определитель  .
.
Решение. Разложим определитель по элементам второй строки:

Примеры для самостоятельной работы
Вычислить определители третьего порядка:
1.  2.
2.  3.
3. 
4. 
 6.
6. 
7. 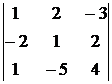 8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
16.  17.
17.  18.
18. 
19.  20.
20.  21.
21. 
22.  23.
23.  24.
24. 
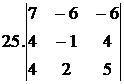 26.
26.  27.
27. 
28.  29.
29. 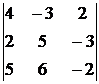 30.
30. 
Задание №2
Пример 3. Пользуясь правилом умножения матриц, представить в виде определителя произведение определителей  .
.
Решение.

Примеры для самостоятельной работы
Пользуясь правилом умножения матриц, представить в виде определителя произведение определителей:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 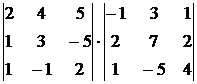
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17. 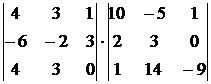 18.
18. 
19.  20.
20. 
21.  22.
22. 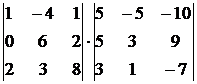
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
Задание №3
Пример 4. Найти обратную матрицу для матрицы  .
.
Решение. Вычислим определитель матрицы
 .
.
Определитель det А ¹0, следовательно, матрица А имеет обратную.
Составим транспонированную матрицу АТ для матрицы А:
 .
.
Найдем алгебраические дополнения элементов матрицы АТ:

Тогда матрица, составленная из алгебраических дополнений матрицы АТ, запишется в виде:  .
.
Запишем обратную матрицу:
 .
.
Покажем, что А × А -1= Е.
Действительно,
 .
.
Примеры для самостоятельной работы
Найти обратную матрицу для матрицы:
1.  2.
2.  3.
3. 
4.  5.
5.  6.
6. 
7.  8.
8.  9.
9. 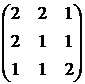
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
16.  17.
17. 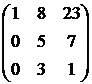 18.
18. 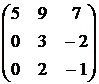
19.  20.
20.  21.
21. 
22.  23.
23.  24.
24. 
25. 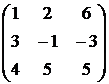 26.
26.  27.
27. 
28.  29.
29.  30.
30. 
Задание № 4
Пример 5. Решить методом Крамера систему уравнений
 .
.
Решение. Вычислим определитель системы
 .
.
Следовательно, система имеет единственное решение. Найдем Dх1, Dх2, Dх3.

Определим решение системы уравнений по формулам Крамера:

Примеры для самостоятельной работы
Решить систему уравнений по правилу Крамера:
1.  2.
2. 
3. 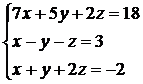



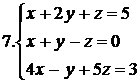










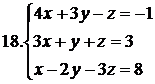






 26.
26. 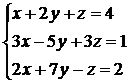
27. 

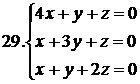

Задание № 5
Скалярное произведение векторов
Скалярным произведением двух векторов  и
и  называется число, равное произведению длин векторов на косинус угла между ними:
называется число, равное произведению длин векторов на косинус угла между ними:
 .
.
Свойства скалярного произведения.
1. 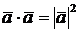 или
или  .
.
2.  , если
, если  , либо
, либо  , либо
, либо  ┴
┴  (ортогональность ненулевых векторов).
(ортогональность ненулевых векторов).
3. Переместительный закон:  .
.
4. Распределительный закон:  .
.
5. Сочетательный закон по отношению к скалярному множителю:
 .
.
Скалярное произведение ортов осей координат:
 ,
,  .
.
Пусть векторы  и
и  заданы своими координатами:
заданы своими координатами: 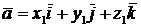 ,
, 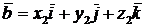 . Тогда скалярное произведение этих векторов находится по формуле:
. Тогда скалярное произведение этих векторов находится по формуле:  .
.
Отсюда следует необходимое и достаточное условие перпендикулярности векторов:  .
.
Угол 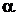 между векторами
между векторами  и
и  определяется формулой
определяется формулой  или в координатах
или в координатах

 2018-03-09
2018-03-09 133
133







