1. Смешанное произведение трех векторов равно нулю, если:
а) хоть один из перемножаемых векторов равен нулю;
б) два из перемножаемых векторов коллинеарны;
в) три ненулевых вектора параллельны одной и той же плоскости (компланарность).
2. Смешанное произведение не изменяется, если в нем поменять местами знаки векторного и скалярного произведения, то есть 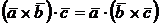 . В силу этого свойства смешанное произведение векторов
. В силу этого свойства смешанное произведение векторов  ,
,  и
и  можно записывать в виде
можно записывать в виде 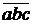 .
.
3. Смешанное произведение не изменяется, если переставлять перемножаемые векторы в круговом порядке: 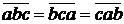 .
.
4. При перестановке любых двух векторов смешанное произведение изменяет только знак: 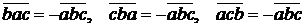 .
.
Пусть векторы заданы их разложением по ортам: 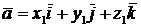 ,
, 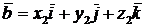 ,
, 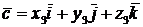 . Тогда
. Тогда
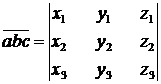 .
.
Из свойств смешанного произведения трех векторов вытекает следующее:
- необходимым и достаточным условием компланарности трех векторов служит условие 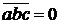 ;
;
- объем 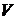 параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах  ,
,  и
и  , равен:
, равен: 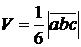 .
.
Решение типовых примеров
Пример 8. Компланарны ли векторы  ,
,  и
и  , если
, если  (-1, 5, 1),
(-1, 5, 1),
 (-1, 3, -1),
(-1, 3, -1),  (2, 0, 2)?
(2, 0, 2)?
Решение. Необходимым и достаточным условием компланарности трех векторов  ,
,  и
и  является равенство нулю их смешанного произведения, то есть
является равенство нулю их смешанного произведения, то есть 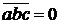 .
.
Находим смешанное произведение векторов  ,
,  ,
, 
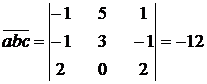 .
.
Так как смешанное произведение векторов не равно нулю, то заданные векторы  ,
,  и
и  не компланарны.
не компланарны.
Ответ. Векторы  ,
,  и
и  не компланарны.
не компланарны.
Примеры для самостоятельного решения
Компланарны ли векторы  ,
,  и
и  ?
?
7.1  (2, 3, 1),
(2, 3, 1),  (-1, 0, -1),
(-1, 0, -1),  (2, 2, 2).
(2, 2, 2).
7.2  (3, 2, 1),
(3, 2, 1),  (2, 3, 4),
(2, 3, 4),  (3, 1, -1).
(3, 1, -1).
7.3  (1, 5, 2),
(1, 5, 2),  (-1, 1, -1),
(-1, 1, -1),  (1, 1, 1).
(1, 1, 1).
7.4  (1, -1,-3),
(1, -1,-3),  (3, 2, 1),
(3, 2, 1),  (2, 3, 4).
(2, 3, 4).
7.5  (3, 3, 1),
(3, 3, 1),  (1, -2, 1),
(1, -2, 1),  (1, 1, 1).
(1, 1, 1).
7.6  (3, 1, -1),
(3, 1, -1),  (-2, -1, 0),
(-2, -1, 0),  (5, 2, -1).
(5, 2, -1).
7.7  (4, 3, 1),
(4, 3, 1),  (1, -2, 1),
(1, -2, 1),  (2, 2, 2).
(2, 2, 2).
7.8  (4, 3, 1),
(4, 3, 1),  (6, 7, 4),
(6, 7, 4),  (2, 0, -1).
(2, 0, -1).
7.9  (3, 2, 1),
(3, 2, 1),  (1, -3, -7),
(1, -3, -7),  (1, 2, 3).
(1, 2, 3).
7.10  (3, 7, 2),
(3, 7, 2),  (-2, 0, -1),
(-2, 0, -1),  (2, 2, 1).
(2, 2, 1).
7.11  (1, -2, 6),
(1, -2, 6),  (1, 0, 1),
(1, 0, 1),  (2, -6, 17).
(2, -6, 17).
7.12  (6, 3, 4),
(6, 3, 4),  (-1, -2, -1),
(-1, -2, -1),  (2, 1, 2).
(2, 1, 2).
7.13  (7, 3, 4),
(7, 3, 4),  (-1, -2, -1),
(-1, -2, -1),  (4, 2, 4).
(4, 2, 4).
7.14  (2, 3, 2),
(2, 3, 2),  (4, 7, 5),
(4, 7, 5),  (2, 0, -1).
(2, 0, -1).
7.15  (5, 3, 4),
(5, 3, 4),  (-1, 0, -1),
(-1, 0, -1),  (4, 2, 4).
(4, 2, 4).
7.16  (3, 10, 5),
(3, 10, 5),  (-2, -2, -3),
(-2, -2, -3),  (2, 4, 3).
(2, 4, 3).
7.17  (-2, -4, -3),
(-2, -4, -3),  (4, 3, 1),
(4, 3, 1),  (6, 7, 4).
(6, 7, 4).
7.18 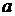 (3, 1, -1),
(3, 1, -1),  (1, 0, -1),
(1, 0, -1),  (8, 3, -2).
(8, 3, -2).
7.19  (4, 2, 2),
(4, 2, 2),  (-3, -3, -3),
(-3, -3, -3),  (2, 1, 2).
(2, 1, 2).
7.20  (4, 1, 2),
(4, 1, 2),  (9, 2, 5),
(9, 2, 5),  (1, 1, -1).
(1, 1, -1).
7.21  (5, 3, 4),
(5, 3, 4),  (4, 3, 3),
(4, 3, 3),  (9, 5, 8).
(9, 5, 8).
7.22  (3, 4, 2),
(3, 4, 2),  (1, 1, 0),
(1, 1, 0),  (8, 11, 6).
(8, 11, 6).
7.23  (4, -1, -6),
(4, -1, -6),  (1, -3,-7),
(1, -3,-7),  (2, -1,-4).
(2, -1,-4).
7.24  (3, 1, 0),
(3, 1, 0),  (-5, -4, -3),
(-5, -4, -3),  (4, 2, 4).
(4, 2, 4).
7.25  (3, 0, 3),
(3, 0, 3),  (8, 1, 6),
(8, 1, 6),  (1, 1, -1).
(1, 1, -1).
7.26  (2, 3, -1),
(2, 3, -1),  (1, -1, 3),
(1, -1, 3),  (1, 9, -11).
(1, 9, -11).
7.27  (2, -1, 3),
(2, -1, 3),  (1, 1, 1),
(1, 1, 1),  (0, 0, 5).
(0, 0, 5).
7.28  (5, 8, -4),
(5, 8, -4),  (6, 9, -5),
(6, 9, -5),  (4, 7, -3).
(4, 7, -3).
7.29  (1, 2, 1),
(1, 2, 1),  (-2, 1, 3),
(-2, 1, 3),  (1, 3, 2).
(1, 3, 2).
7.30  (2, 3, 1),
(2, 3, 1),  (-2, 0, 2),
(-2, 0, 2),  (0, 2, 1).
(0, 2, 1).
Задание № 8
Решение типовых примеров
Пример 9. Найти производные данных функций:
а) 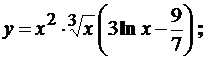 б)
б) 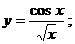 в)
в) 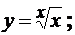
г) 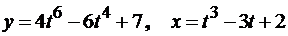 .
.
Решение:
а) Перепишем заданную функцию в виде 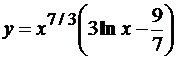 .
.
Тогда 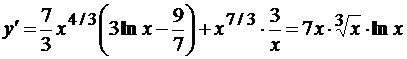 .
.
б) 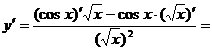
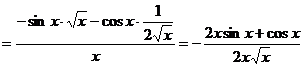 .
.
в) Перепишем заданную функцию в виде 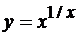 . Здесь основание и показатель степени зависят от x. Логарифмируя, получим
. Здесь основание и показатель степени зависят от x. Логарифмируя, получим 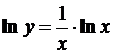 . Продифференцируем обе части равенства по x. Так как у является функцией от x, то ln y есть сложная функция x и
. Продифференцируем обе части равенства по x. Так как у является функцией от x, то ln y есть сложная функция x и 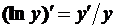 . Следовательно,
. Следовательно,
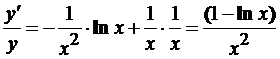 ,
,
Т.е.
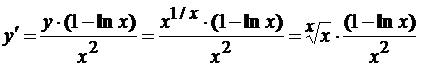 .
.
|
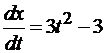 ,
, 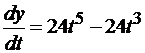 . Следовательно,
. Следовательно, 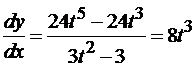 .
.
Найти производные данных функций:
8.1 а) 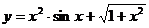 ;
;
б) 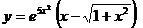 ;
;
в) 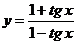 ;
;
г) 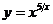 ;
;
д) 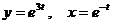 .
.
8.2 а) 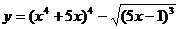 ;
;
б) 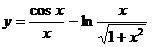 ;
;
в) 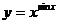 ;
;
г)
|
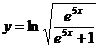 ;
;
д) 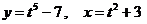 .
.
8.3 а) 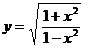 ;
;
б) 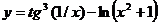 ;
;
в) 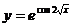 ;
;
г) 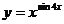 ;
;
д) 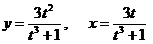 .
.
8.4 а) 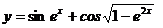 ;
;
б) 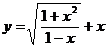 ;
;
в) 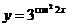 ;
;
г) 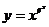 ;
;
д) 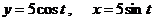 .
.
8.5 а) 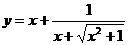 ;
;
|
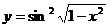 ;
;
в) 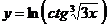 ;
;
г) 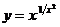 ;
;
д) 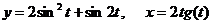 .
.
8.6 а) 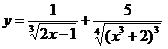 ;
;
б) 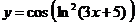 ;
;
в) 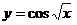 ;
;
г) 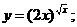
д) 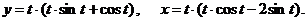
8.7 а) 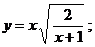
б) 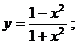
в) 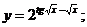
г) 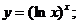
д) 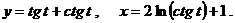
8.8
|
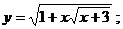
б) 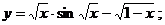
в) 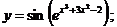
г) 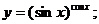
д) 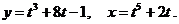
8.9 а) 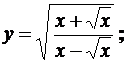
б) 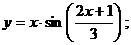
в) 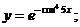
г) 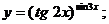
д) 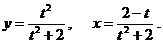
8.10 а) 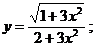
б) 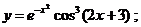
в) 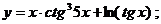
|
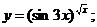
д) 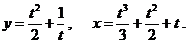
8.11 а) 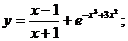
б) 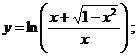
в) 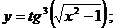
г) 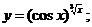
д) 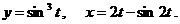
8.12 а) 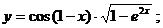
б) 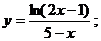
в) 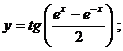
г) 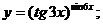
д) 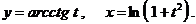
8.13 а) 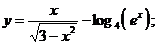
б) 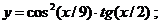
в) 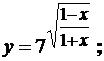
г) 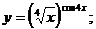
д) 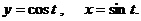
8.14 а) 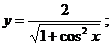
б) 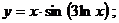
в) 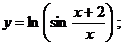
г) 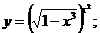
д) 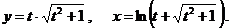
8.15 а) 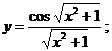
|
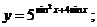
в) 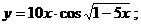
г) 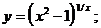
д) 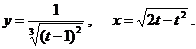
8.16 а) 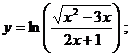
б) 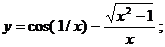
в) 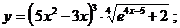
г) 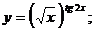
д) 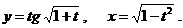
8.17 а) 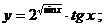
б) 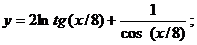
в) 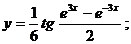
|
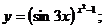
д) 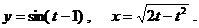
8.18 а) 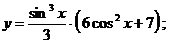
б) 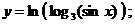
в) 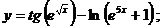
г) 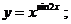
д) 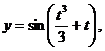
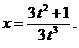
8.19 а) 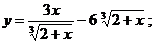
б) 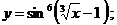
в) 
г) 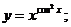
д) 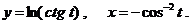
8.20
|
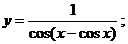
б) 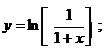
в) 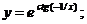
г) 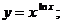
д) 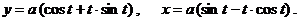
8.21 а) 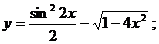
б) 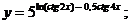
в) 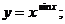
г) 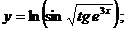
д) 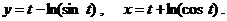
8.22 а) 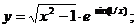
б) 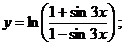
в) 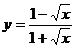
|
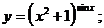
д) 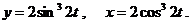
8.23 а) 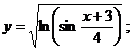
б) 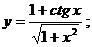
в) 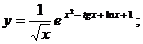
г) 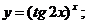
д) 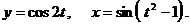
8.24 а) 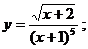
б) 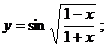
в) 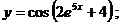
г) 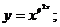
д) 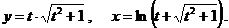
8.25
|
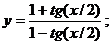
б) 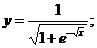
в) 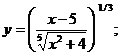
г) 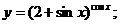
д) 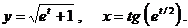
 2018-03-09
2018-03-09 132
132







