2018-03-09
110
Пример 6. Найти косинус угла между векторами 
и 
, если даны координаты точек А (2, -1, 0), В (3, -1, 2), С (1, -2, 3).
Решение. Вычислим координаты векторов 
и 
:
;
.
Определим скалярное произведение векторов и как сумму произведений их одноименных координат:
.
Найдем длины векторов: 
и 
.
Вычислим косинус угла между векторами и :
.
Ответ. 
.
Примеры для самостоятельного решения
Найти косинус угла между векторами 
и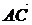 
.
5.1 А (1, -2, 3), В (0, -1, 2), С (3, -4, 5).
5.2 А (0, -3, 6), В (-12, -3, -3), С (-9, -3, -6).
5.3 А (3, 3, -1), В (5, 5, -2), С (4, 1, 1).
5.4 А (-1, 2, -3), В (3, 4, -6), С (1, 1, -1).
5.5 А (-4, -2, 0), В (-1, -2, 4), С (3, -2, 1).
5.6 А (5, 3, -1), В (5, 2, 0), С (6, 4, -1).
5.7 А (-3, -7, -5), В (0, -1, -2), С (2, 3, 0).
5.8 А (2, -4, 6), В (0, -2, 4), С (6, -8, 10).
5.9 А (0, 1, -2), В (3, 1, 2), С (4, 1, 1).
5.10 А (3, 3, -1), В (1, 5, -2), С (4, 1, 1).
5.11 А (2, 1, -1), В (6, -1, -4), С (4, 2, 1).
5.12 А (-1, -2, 1), В (-4, -2, 5), С (-8, -2, 2).
5.13 А (6, 2, -3), В (6, 3, -2), С (7, 3, -3).
5.14 А (0, 0, 4), В (-3, -6, 1), С (-5, -10, -1).
5.15 А (2, -8, -1), В (4, -6, 0), С (-2, -5, -1).
|
|
|
5.16 А (3, -6, 9), В (0, -3, 6), С (9, -12, 15).
5.17 А (0, 2, -4), В (8, 2, 2), С (6, 2, 4).
5.18 А (3, 3, -1), В (5, 1, -2), С (4, 1, 1).
5.19 А (-4, 3, 0), В (0, 1, 3), С (-2, 4, -2).
5.20 А (1, -1, 0), В (-2, -1, 4), С (8, -1, -1).
5.21 А (7, 0, 2), В (7, 1, 3), С (8, -1, 2).
5.22 А (2, 3, 2), В (-1, -3, -1), С (-3, -7, -3).
5.23 А (2, 2, 7), В (0, 0, 6), С (-2, 5, 7).
5.24 А (-1, 2, -3), В (0, 1, -2), С (-3, 4, -5).
5.25 А (0, 3, -6), В (9, 3, 6), С (12, 3, 3).
5.26 А (3, 2, -3), В (5, 1, -1), С (1, -2, 1).
5.27 А (-1, -2, 4), В (-4, -2, 0), С (3, -2, 1).
5.28 А (1, 2, 1), В (3, -1, 7), С (7, 4, -2).
5.29 А (1, -1, -3), В (0, 1, -1), С (-1, 0, -5).
5.30 А (-3, -1, 3), В (-2, 1, 1), С (-1, 0, 5).
Задание № 6
Векторное произведение
Векторным произведением вектора 
на вектор 
называется третий вектор 
, определяемый следующим образом:
1. модуль вектора равен площади параллелограмма, построенного на векторах и (
, где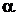 
– угол между векторами
и 
);
2. вектор 
перпендикулярен векторам и ;
3. векторы , , после приведения к общему началу ориентированы по отношения друг к другу соответственно как орты 
, 
, 
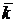(в правой системе координат образуют так называемую правую тройку векторов).
Векторное произведение на обозначается через 
.
Свойства векторного произведения.
1. Векторное произведение не обладает переместительным свойством, то есть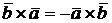 
.
2. 
, если 
, либо 
, либо ║ (коллинеарность ненулевых векторов).
3. Сочетательное свойство по отношению к скалярному множителю: 
.
4. Распределительное свойство: 
.
Векторное произведение координатных ортов , и :
, 
.
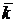Векторное произведение векторов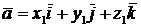 
и
|
|
|
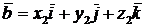удобнее находить по формуле: 
.
Отсюда следует, что модуль векторного произведения равен площади параллелограмма, построенного на векторах и :
.
Тогда площадь треугольника, построенного на векторах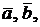 
находится по формуле:
.
Векторное произведение обращается в нуль тогда и только тогда, когда векторы на коллинеарны или один из векторов 
(или ) нулевой.
