II. Признак Даламбера (в предельной форме)

Теорема 1. Если для ряда 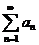  с положительными членами существует конечный предел  (1) отношения (n+1)-го члена к n-му, то

а) при Д<1 ряд расходится, а

б) при Д>1 – расходится.

Доказательство.

а) Пусть Д<1. Возьмем любое число q, удовлетворяющее неравенствам 0<Д<q<1

Тогда из соотношения следует, что существует такое натуральное число N, что для всех значений  будет справедливо неравенство

В последнем неравенстве полагаем n=N, N+1, …

 (2)

или  (2^/)

Рассмотрим теперь два ряда:

 (3) и

 (4).

Ряд (4) сходится (как геометрический ряд со знаменателем ). Члены же положительного ряда (3) как показывают неравенства (2^/), меньше соответствующих членов ряда (4). Следовательно, на основании принципа сравнения рядов этот ряд также сходится.

Но тогда сходится и данный ряд 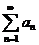 (на основании теоремы о сходимости остатка ряда), т. к. ряд (3) представляет собой N-й остаток ряда .

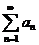б) Пусть теперь Д>1.

Тогда из соотношения 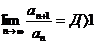следует, что начиная с некоторого номера N, будет иметь место неравенство  

Последнее неравенство означает, что члены ряда 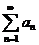, начиная с номера N, образуют возрастающую последовательность положительных чисел и, следовательно, общий член этого ряда не стремится к нулю при .

Но в таком случае в силу следствия из необходимого признака сходимости ряд расходится.

 

Пример. Выяснить, сходится ли ряд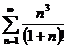

Имеем:

на основании признака Даламбера данный ряд сходится.

 

Пример 2.

Имеем:

Т. к. , то ряд расходится.

 

Замечание 1. В тех случаях, когда 1)  или 2) не существует признак Даламбера ответа не дает на вопрос о том, сходится или расходится ряд.

При этом ряд может оказаться как сходящимся, так и расходящимся. В этом, так называемом, сомнительном случае вопрос о характере данного ряда приходится решать как-либо иначе.

Пример.

. Признак Даламбера ответа не дает на вопрос о сходимости данного ряда. Между тем принцип сравнения рядов решает этот вопрос: 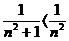 при всех значениях n, а ряд с общим членом  сходится. Следовательно, данный ряд сходится.

 

Замечание 2. Ряд 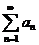 будет расходится и в том случае, когда

 

Пример.

. следовательно, данный ряд расходится.