2018-03-09
115
Теорема. Если для положительного ряда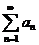 
существует конечный предел 
, то
а) при С<1 ряд сходится, а
б) при С>1 – расходится.
Доказательство производится аналогично признаку Даламбера (см. Увар., т. 2,стр. 24)
Пример. 
- ряд сходится.
Замечание 1. Если 
, то ряд будет расходится.
Замечание 2. Если 
1) не существует или 2) равен 1, то признак Коши, как и признак Даламбера, не дает ответа на вопрос о сходимости ряда.
IV. Интегральный признак Коши
Признаки Даламбера и Коши не всегда являются эффективными при исследовании характера данного ряда.
Рассмотрим еще один признак, который позволяет иногда решать вопрос о сходимости ряда с положительными членами в тех случаях, когда рассмотренные выше признаки оказываются непригодными.
Этот признак основан на сравнении данного ряда с некоторым несобственным интегралом I рода от функции 
, значения которой при последовательных целых значениях аргумента дают все члены этого ряда.
Теорема. Дан положительный ряд 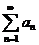(1); если существует не возрастающая непрерывная ф-ия , где 
, такая, что 
, то
1) ряд (1) сходится, если сходится несобственный интеграл 
; и
2) расходится, если этот интеграл расходится.
Доказательство: рассмотрим криволинейную трапецию, ограниченную линией 
, где - непрерывная, невозрастающая функция, с основанием от х=1 до х=n.
