I. Признаки сравнения рядов

Теорема 1. Пусть даны два положительных ряда 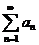 (1) и (2). Если члены ряда (1) не превосходят соответствующих членов ряда (2), т. е. (n=1, 2, 3), и ряд (2) сходится, то ряд (1) также сходится.

Доказательство. Пусть S_n частичная сумма ряда (1), s_n – частичная сумма ряда (2). Предположим, что  для " n=1, 2, 3. Тогда, очевидно, и частичные суммы рядов связаны неравенствами того же смысла: (3).

Пусть ряд (2) сходится, тогда , но   (последовательность частичных сумм положительного ряда есть всегда возрастающая последовательность). Из неравенства (3) следует, что  (4)

По теореме о пределе возрастающей ограниченной последовательности из неравенства (4) следует, что существует предел S_n, а это означает, что ряд (1) сходится.

Теорема 2. Пусть даны два положительных ряда 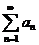  (1) и  (2). Если члены ряда (1) не меньше соответствующих членов ряда (2), т. е. (n=1, 2, 3), и ряд (2) расходится, то ряд (1) также расходится.

Доказательство. Пусть  (" n=1, 2, 3). Тогда 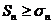 (5).

Т. к. s_n- возрастающая последовательность и т. к. ряд (2) расходится, то

В силу неравенства (5): что означает расходимость ряда (1).

Замечание. Признаки сравнения применимы и в том случае, когда условие  (или ) выполняется не при всех n, а лишь начиная с некоторого n=N. Это следует из теоремы о сходимости остатка ряда.

 

Пример 1. Исследовать на сходимость ряд

Оценим общий член данного ряда:  . Ряд с общим членом b_n=1/2ⁿ. сходится (геометрический ряд). По теореме 1 данный ряд также сходится.

 

Пример 2. Исследовать на сходимость ряд

Оценим общий член данного ряда: a_n=

Последний ряд  расходится (как узнаете позднее, это гармонический ряд). Следовательно по теореме 1 данный ряд так же расходится.

 

Отметим полезное следствие из доказанных выше теорем 1 и 2.

Теорема(*). Пусть даны два положительных ряда 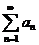 (1)  и  (2). Если существует конечный, отличный от нуля, предел отношения общих членов этих рядов:  , то оба ряда сходятся или расходятся одновременно.

Смысл этого следствия состоит в том, что если общий член ряда (1) и общий член ряда (2) являются бесконечно малыми (если общие члены этих рядов стремятся к нулю при , то a_n и b_n можно рассматривать как бесконечно малые) одного и тогоже порядка (при )то сходимость одного из этих рядов влечет сходимость другого (а значит, и,наоборот, расходимость одного влечет расходимость другого).

Эту теорему можно прочитать следующим образом:

Если два ряда имеют общие члены одинакового порядка малости (при ), то эти ряды сходятся или расходятся одновременно.

Замечание. В случае расходимости предел отношения А может равняться ¥ (см. Уваренков, стр. 20).

При практическом использовании теоремы (*) поступают следующим образом:

Находят более простую бесконечно малую того же порядка малости (при ), что и общий член исследуемого ряда.

 

Пример 1.  .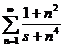

 при  . Поэтому можно ставить вопрос о том, сходится ли данный ряд. Возьмем

 

т. к. ряд   сходится (что будет доказано позднее!!!),то и данный ряд сходится.

 

Пример 2.  

Имеем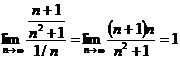

Т. к. ряд с общим членом 1/n (гармонический ряд) расходится, то и теорема (*) будет расходится и данный ряд.

 

Заключение о сходимости или расходимости какого-либо данного ряда практически не всегда удобно делать на основании принципа сравнения рядов, т. к. нет никаких общих правил для подбора подходящего ряда, сходимость или расходимость которого уже известна и сравнение с которым дало бы ответ на вопрос о сходимости или расходимости исследуемого ряда: все зависит от навыка исследователя, в частности от запаса известных ему сходящихся, расходящихся рядов.

Поэтому возникает необходимость установить признаки, которые позволяли бы в большом числе случаев судить о сходимости или расходимости данного ряда, без привлечения других вспомогательных рядов.