Когда можно пользоваться рассмотренным инструментом и как пользоваться?
ЧИСЛОВЫЕ РЯДЫ
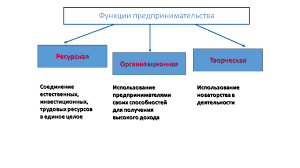
Основной задачей математического анализа является изучение функций. Дифференциальное исчисление позволяет изучать многие вопросы, связанные с теми или иными свойствами функции 9возрастание и убывание, экстремумы, точки перегиба, приближенное вычисление значений функции и др.). Те мне менее с помощью только дифференциального исчисления невозможно изучить многие проблемы математического анализа. Они успешно решаются на основании теории рядов.
Основные понятия
Пусть дана бесконечная числовая последовательность: a1, a2, a3,…, an,…
Выражение, которое получится, если все члены этой последовательности соеденить формально знаком плюс:
 , (1)
, (1)
называется числовым рядом (или просто рядом). Часто ряд записывают в виде 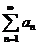 , где указано, что индекс n пробегает все натуральные числа: 1, 2, 3,….
, где указано, что индекс n пробегает все натуральные числа: 1, 2, 3,….
Числа a1, a2, a3,…, an,… называются членами ряда, 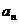 называют общим членом ряда (при произвольном n!!).
называют общим членом ряда (при произвольном n!!).
В арифметике и алгебре рассматривают суммы с конечным числом слагаемых. В ряде же слагаемых бесконечно много. Поэтому понятие суммы, состоящей из бесконечного числа слагаемых, требует некоторого специального определения. Что же понимают под выражением (1)?
Может оказаться, что иногда это выражение и лишнего чистого смысла.
Введем тонкое определение.
Возьмем сумму n первых членов ряда (1) и обозначим ее через Sn:
 (2)
(2)
эту сумму называют n-й частичной суммой ряда (1). При этом под S1 понимают a1.
Давая в (2) «n» последовательных значений 1, 2, 3,…, получим последовательность частичных сумм:



Возможны два случая:
1) либо эта последовательность имеет конечный предел
2) либо она не имеет конечного предела (стремится к ¥ или вовсе не стремится
ни к какому пределу).
Определение. Если последовательность частичных сумм (или иначе частичная сумма Sn) имеет конечный предел  , то ряд (1) называется сходящимся, а сам этот предел называется суммой ряда.
, то ряд (1) называется сходящимся, а сам этот предел называется суммой ряда.
При этом пишут:  или
или  .
.
Если же последовательность частичных сумм не имеет предела то ряд (1) называется расходящимся.
Расходящийся ряд не имеет суммы в том смысле как мы ее определили.
Однако в том случае когда  , пишут
, пишут  , а также S=¥.
, а также S=¥.
Пример 1. Пользуясь непосредственно определением суммы ряда, показать, что ряд  сходится и найти его сумму.
сходится и найти его сумму.
Представим общий член ряда в виде суммы двух дробей:

Тогда частичную сумму Sn данного ряда можем переписать так:

В соответствии с определением надо выяснить существует ли конечный предел Sn при n®¥:

следовательно данный ряд сходится и его сумма S=1.
Замечание. В большинстве случаев не удается найти общей формулы для Sn, поэтому вопрос о существовании конечной суммы ряда (т. е. вопрос о сходимости ряда) приходится решать косвенным путем, используя признаки сходимости).

Решение. 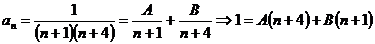 n=-1; A=1/3; B=-1/3.
n=-1; A=1/3; B=-1/3.
Sn-? 

Пример 2. Исследование сходимости ряда, составленного из членов геометрической прогрессии.
Рассмотрим ряд
 , (3)
, (3)
составленный из членов геометрической прогрессии. Часто данный ряд называют геометрическим рядом.
Выясним, при каких значениях q ряд (3) сходится.
Составим частичную сумму Sn ряда:
 по формуле для суммы n первых членов геометрической прогрессии=
по формуле для суммы n первых членов геометрической прогрессии=  (4)
(4)
Очевидно что при n®¥ изменяется только второе слагаемое последней формулы, причем характер его изменения зависит от того, каково число q.
а) если 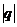 <1 (прогрессия убывающая), то
<1 (прогрессия убывающая), то 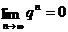 , поэтому
, поэтому  существует и
существует и 

следовательно, в случае, когда 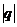 <1, ряд (3) сходится и его сумма равна
<1, ряд (3) сходится и его сумма равна  .
.
б) Если 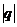 >1, то
>1, то  , а тогда (т. к. a¹0) и
, а тогда (т. к. a¹0) и 

Значит, в случае, когда 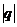 >1, ряд (3) расходится.
>1, ряд (3) расходится.
в) если q=-1, то частичная сумма Sn принимает вид: 
Отсюда ясно что в этом случае Sn при n®¥ предела не имеет и ряд (3) расходится.
г) При q=1 формула (4) лишена смысла. Но ясно непосредственно, что в этом случае

Значит в случае q=1 ряд (3) также расходитс я.
Вывод. Итак геометрический ряд 1) сходится при 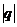 <1 и 2) расходится
<1 и 2) расходится 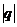 ³1 (a¹0), причем при
³1 (a¹0), причем при 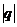 <1 имеем известную (из школьного курса математики) формулу суммы членов бесконечной убывающей геометрической прогрессии.
<1 имеем известную (из школьного курса математики) формулу суммы членов бесконечной убывающей геометрической прогрессии.
ПРОСТЕЙШИЕ СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
Теорема 1. Если ряд 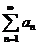 (1) сходится и имеет сумму S, то ряд
(1) сходится и имеет сумму S, то ряд 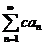 (2) (где С – какая-либо постоянная) также сходится и имеет сумму cS.
(2) (где С – какая-либо постоянная) также сходится и имеет сумму cS.
Доказательство: Возьмем n-ю частичную сумму ряда 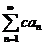 :
: 
где 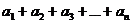 - n-я частичная сумма Sn ряда
- n-я частичная сумма Sn ряда 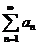 .
.
Поэтому, т. к. по условию  ,
,  ,существует так, что ряд
,существует так, что ряд 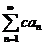 сходится, причем
сходится, причем 
Итак, если все члены данного сходящегося ряда умножить на одно и тоже число С, то сходимость этого ряда не нарушится, а сумма его умножится на тоже число: s=с×S.
Таким образом, сходящиеся ряды подчиняются (подобно конечным суммам) дистрибутивному закону умножения (так что в сходящемся ряде можно выносить за скобки общий множитель всех членов ряда).
Теорема 2. Если ряды 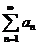 (1) и
(1) и  (2) сходятся и имеют соответственно суммы S и s, то ряды
(2) сходятся и имеют соответственно суммы S и s, то ряды  (3) и
(3) и  (4) также сходятся и их суммы соотвественно равны S+s и S-s.
(4) также сходятся и их суммы соотвественно равны S+s и S-s.
Доказательство: докажем, например, сходимость ряда (3). Возьмем частичную сумму этого ряда:

т. к. 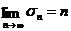 ,
,  - по условию теории, что и доказывает утверждение теоремы для ряда (3).
- по условию теории, что и доказывает утверждение теоремы для ряда (3).
Аналогично доказывается, что ряд (4) так же сходится и что его сумма равна S-s.
Относительно рядов (3) и (4) говорят, что они получены в результате почленного сложения или соотвественно почленного вычитания рядов (1) и (2), и доказанную теорему часто формулируют так: почленное сложение (вычитание) двух сходящихся рядов дает снова сходящийся ряд, и сумма нового ряда получается сложением (вычитанием) сумм двух данных рядов.
Вывод. Таким образом: 1) сходящиеся ряды можно почленно складывать и вычитать так же, как и конечные суммы; 2) можно умножать члены сходящегося ряда на одно и тоже постоянное число, в результате получаются так же сходящиеся ряды.
Замечание. Если ряды (1) и (2) оба расходятся, то о рядах (3) и (4) в общем случае ничего сказать нельзя. Они могут оказаться как сходящимися, так и расходящимися.
Пример. Найти сумму ряда:

По теореме 2:

ОСТАТОК РЯДА
Пусть дан ряд:  (1). Отбросим любое фиксированное число «k» его первых членов, тогда получим новый ряд
(1). Отбросим любое фиксированное число «k» его первых членов, тогда получим новый ряд  (2).
(2).
Определение. Ряд (2), который получается из данного ряда (1) путем отбрасывания некоторого конечного числа членов, взятых подряд начиная с первого, называется остатком данного ряда.
Если отброшено k первых членов, то остаток называется k-м остатком и его можно записать в виде суммы  .
.
По своему поведению ряды (1) и (2) тесно связаны.
Теорема. Ряды (1) и (2): 1) либо одновременно сходятся 2) либо одновременно расходятся.
Доказательство.
1) Пусть Sk – сумма k первых членов ряда (1), sn – сумма n первых членов ряда (2). Тогда, очевидно, что
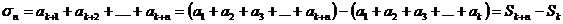 , т. е.
, т. е.

Предположим, что ряд (1) сходится, и пусть  , а следовательно, и
, а следовательно, и  (5), ибо при n®¥ и (n+k)®¥.
(5), ибо при n®¥ и (n+k)®¥.
Тогда из равенства (3) находим, что
 , т. е.
, т. е.
предел частичной суммы ряда (2) существует и равен S-Sk, а это означает, что ряд (2) так же сходится и сумма его равна S-Sk (Sk – фиксированное число, не зависящее от n).
3) Предположим теперь, что сходится ряд (2), и пусть 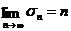 .
.
В таком случае из равенства (4) имеем:
 , т. е. предел частичной суммы Sn+k ряда (1) существует и равен s+Sk, а это означает, что ряд (1) тоже сходится и его сумма равна s+Sk.
, т. е. предел частичной суммы Sn+k ряда (1) существует и равен s+Sk, а это означает, что ряд (1) тоже сходится и его сумма равна s+Sk.
3) Если же один из двух рядов (1) или (2) расходитс я, то и второй не может сходится, т. к. иначе по доказанному сходился бы и первый.
Вывод. Таким образом: 1) если сходится данный ряд 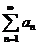 , то сходится и любой его отстаток; 2) если сходится какой-либо остаток ряда, то сходится и сам ряд.
, то сходится и любой его отстаток; 2) если сходится какой-либо остаток ряда, то сходится и сам ряд.
Следствие: Ряды 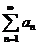 (6) и
(6) и  (7), у которых лишь конечное число членов отличается друг от друга, либо одновременно сходятся, либо одновременно расходятся.
(7), у которых лишь конечное число членов отличается друг от друга, либо одновременно сходятся, либо одновременно расходятся.
Д-но, если, например,  , начиная с n>k, то ряды (6) и (7) сходятся или расходятся одновременно с рядом (2):
, начиная с n>k, то ряды (6) и (7) сходятся или расходятся одновременно с рядом (2):

Таким образом, отбрасывание конечного числа членов ряда (или добавление к ряду конечного числа членов) не влияет на сходимость или расходимость этого ряда.
Поэтому при исследовании ряда на сходимость можно: 1) изменять конечное число членов этого ряда, а так же 2) добавлять или 3) отбрасывать конечное число членов.
Замечание. Разумеется, сумма сходящегося ряда при таких преобразованиях, вообще говоря, изменится.
Пример. Исследовать на сходимость ряд
 (n>4)
(n>4)
Решение. Отбросим в данном ряде 4-ре первых члена, тогда получим новый ряд:
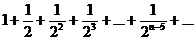 (n=1, 2, 3, …)
(n=1, 2, 3, …)
который сходится как геометрическая прогрессия с  <1. Следовательно, сходится и рассматриваемый ряд.
<1. Следовательно, сходится и рассматриваемый ряд.
 2018-03-09
2018-03-09 418
418